本文关注于采用半监督图编码方法来对图中节点分类，根据上文的介绍，半监督图编码方法有两个过程：节点特征编码和节点分类。本文介绍基于条件随机场的图卷积网络（Graph Convolutional Network with Conditional Random Field, GCN-CRF）模型，关注于优化节点分类过程。GCN-CRF通过在softmax层前添加条件随机场模块来平滑GCN的分类结果。

条件随机场

条件随机场（Conditional Random Field, CRF）已经成功地应用到了图像分割和图像标注等问题上。通常的做法是在像素点或者图像区块上定义条件随机场^{zheng2015conditionalfulkerson2009class}，然后做最大后验（MAP）推理。CRF通过引入一些约束来平滑分类结果，这些约束倾向于减少对象边缘附近的错误分类。全连接CRF已经成功地被用来改善卷积神经网络CNN的语义标记结果^{chen2016deeplab}。接下来本文以图像像素级标注问题为例，简要介绍条件随机场模型。

令$Y_i$为隶属于像素点$i$的随机变量，表示赋予像素点$i$的类别标签。$Y_i$的取值范围为预先定义的标签集合$\mathbb{L} = {l_1, l_2,\cdots, l_c}$ ，$c$为类别的个数。给定一张有$N$个像素点的图像，以及图像的全局观测$X$（每个像素点的特征，这里一般为RGB三通道的值），观测标签对 $(X,Y)$ 可以被建模为一个形式为吉布斯分布 $P(Y=y|X) = \frac{1}{Z(X)} \exp(-E(y|X))$ 的条件随机场。这里$E(y|X)$为标记$y \in \mathcal{L}^N$的Gibbs能量。从现在开始，为了方便起见，我们在公式中去除了条件于$X$，例如用$E(y)$替代$E(y|X)$。

在全连接的成对CRF模型中^{krahenbuhl2011efficient}，类别标签指派$y$的能量由下式给出：

$$E(y) = \sum_{i} \psi_u(y_i) + \sum_{i<j} \psi_p(y_i, y_j) \tag{1}$$

其中$i$和$j$的范围都是从1到$N$。一元能量部分$\psi_u(y_i)$度量像素点$i$的标签分配$y_i$的逆似然（inverse likelihood）。在图像分割中，该一元能量是通过CNN获得的。粗略地说，CNN在预测像素的标签时并未考虑标签分配的平滑性和一致性。 本文采用PyDenseCRF中的方法从分类器输出的类别概率分布计算该一元能量。公式中第二部分的成对（pairwise）能量部分，本文称之为二元能量。二元能量提供像素点间的平滑项，鼓励将相似标签分配给具有相似属性的像素。其常用的定义为加权高斯：

$$\psi_p(y_i, y_j) = \mu (y_i, y_j) \sum_{m=1} ^M w^{(m) } k_G^{ (m) }(f_i, f_j) \tag{2}$$

其中每个$k_G^{(m)}$ 是作用于特征向量的高斯核。像素点$i$的特征向量$f_i$源自图像特征，比如空间位置和RGB值。函数$\mu ( \cdot,\cdot )$为标签兼容性函数，用于捕获不同标签之间的兼容性。最小化上述CRF能量$E(y)$将为图像产生最可能的标签分配$y^*$。

基于条件随机场的图卷积网络

受上述图像中像素级标注任务的启发，本文想要借用成对条件随机场来改善GCN的分类结果，就像图像中采用条件随机场来平滑CNN的结果一样。 基于这个出发点，本章提出了端到端的基于条件随机场的图卷积网络——GCN-CRF（Graph Convolutional Network with Conditional Random Field）神经网络模型。 值得注意的是，图像中的像素点之间是严格的栅格结构，每个像素点周围的像素点的结构是固定的。而且图像中每一小块都是由一堆像素点堆叠组合而成的，所以局部邻近像素点之间存在一定的关联性，但是只考虑一阶邻居，信息量太少，所以之前的工作在所有像素点上构建全连接的成对条件随机场。在实际网络数据中，比如学术网络、社交网络等，网络是任意的二维结构，每个节点的邻居的数量与局部结构都是不一样的。但是与图像中的像素点不同的是，实际网络中的网络结构显示的指定了节点之间的关系。因此，我们可以在实际的网络结构上构建条件随机场。由于实际中网络比较稀疏，相对于全连接的情况，网络中的边的数目大幅度地减少，这使得模型的求解变得更加快速。 由于图片的栅格结构本质上也是一个图结构，本节仍可以采用上一小节CRF的符号定义，接下来的部分将对此详细介绍。

图上条件随机场的定义

相比于图像中的RGB观测值，定义中的$X$此时为节点特征矩阵。节点间的连接关系也从图像中像素点上的全连接变成了图结构$A$。一元能量函数可以从GCN的分类结果中得到。对于二元能量函数，本文借鉴了Krähenbühl^{krahenbuhl2011efficient}中的定义，其定义如下：

$$k(f_i,f_j) = w^{\(1\)} \exp (-\frac{ \|p_i - p_j\|^2 }{ 2\theta_{ \alpha }^2} - \frac{ \|I_i - I_j\|^2 }{ 2\theta_{\beta}^2 } ) + w^{\(2\)} \exp (-\frac{\|p_i - p_j \|^2 }{2 \theta_{\gamma}^2}) \tag{3}$$

其中$I_i$为像素点$i$的RGB三通道颜色值，$p_i$为像素点$i$在图片中二维坐标，因此能比较方便的计算距离，而且距离的计算也具备一定的意义。但是，如果扩展到任意的网络结构数据上，节点到节点之间的距离计算可以通过最短路径的长度来表示，但是可以想象计算量的巨大。像素点的RBG三通道可以扩展成任意维度的节点特征，但是这里需要计算节点间的相似性，开销是平方级的，因此Krähenbühl利用高纬度滤波（High-Dimension Filtering）近似计算将开销降为线性。与图像不同的是，图像的观测是RGB三通道的值，这属于自然观测的ground truth，而非提取出的特征，因此能反映真实情况，具备准确性。然而，如果是基于抽取出来的特征的话，由于特征的抽取会存在特征选取的合理性、抽取过程的准确性等因素，抽取的特征存在太多噪声和不准确性，并不能准确地反映样本的真实观测，因此在抽取的特征上我们无法像公式(3)那样添加特征上的依赖。

综上所述，本质上核函数是为了计算节点之间的相似性，相似性越大，核函数的值越大。由于CRF是加在GCN的后面，要编码的特征已经融合了邻居信息，因此本文的目标是让具有相似特征的邻近节点其标签倾向于相似。同时，为了降低模型的计算复杂度并方便与GCN衔接，本文将二元能量函数定义为：

$$\psi_p(y_i, y_j) = \mu(y_i, y_j)k(f_i, f_j) = \mu(y_i, y_j) \exp( - \frac{ \widehat{A}\_{ij} }{2\alpha^2}) \tag{4}$$

其中$\widehat{A}$为经过图拉普拉斯变换后的邻接矩阵，与GCN中的处理方式保持一致，具体已经在上一章进行了详细的解释。$\widehat{A}$可以视为节点间在结构上的距离。本文也尝试了像公式(3)一样引入在节点特征上的距离的方案，但是实验结果并没有想象的好，因为编码的特征和原始特征都存在误差，不能像RGB颜色一样反映自然观测。因此，本文采纳了公式(3)的定义来提高正确率和减小计算复杂度。

本文采纳了一种简单的标签兼容性函数$\mu$，其定义为$ \mu(y_i, y_j) = [ y_i \neq y_j]$ 。这样的定义方式会给网络结构上邻近但是标签不同的节点对引入惩罚。这种简单的定义方式在实际中产生了较好的效果^{krahenbuhl2011efficientzheng2015conditional}。在GCN的处理过程中，每个节点收集邻居的信息并将其编码进入一个隐空间。如此，有许多共同邻居的邻近节点倾向于拥有相似的特征编码。二元能量函数提供了一个平滑项，该平滑项鼓励将相似类别分配给具备相似编码的邻近节点。

条件随机场的推理算法

介绍了CRF的定义，接下来的是CRF的推理求解。精确地最小化能量$E(y)$是困难的，通常的做法是使用平均场（mean-field）近似推理。 Krähenbühl^{krahenbuhl2011efficient}提出了一种高效的平均场近似推理算法，该算法为一种迭代的消息传播算法。具体的算法步骤总结如下：

注意$k^{(m)}(f_i, f_j)$是第$m$个核函数而且在本文的定义中只有一个核函数。 第一步的初始化，可以看作是在负的一元能量上应用softmax函数，用来做归一化处理。消息传播是通过对$Q$值应用$M$个高斯滤波器来实现的。紧接着对上一步的$M$个高斯滤波的结果进行加权求和，并实施兼容性转换，使加权求和的结果以不同程度在不同标签之间共享。最后加上负的一元能量并再次做归一化。如此循环直到$Q$值收敛。

模型结构

Zheng^{zheng2015conditional}指出，以上条件随机场的平均场推理算法可以重新表述为循环神经网络（Recurrent Neural Network, RNN）的形式，并且将这种RNN结构命名为CRF-RNN。本章使用了一个与CRF-RNN相似的RNN模块，并基于此模块提出了GCN-CRF（Graph Convolutional Network with Conditional Random Field）模型。下图给出了GCN-CRF模型的模型结构的示意图。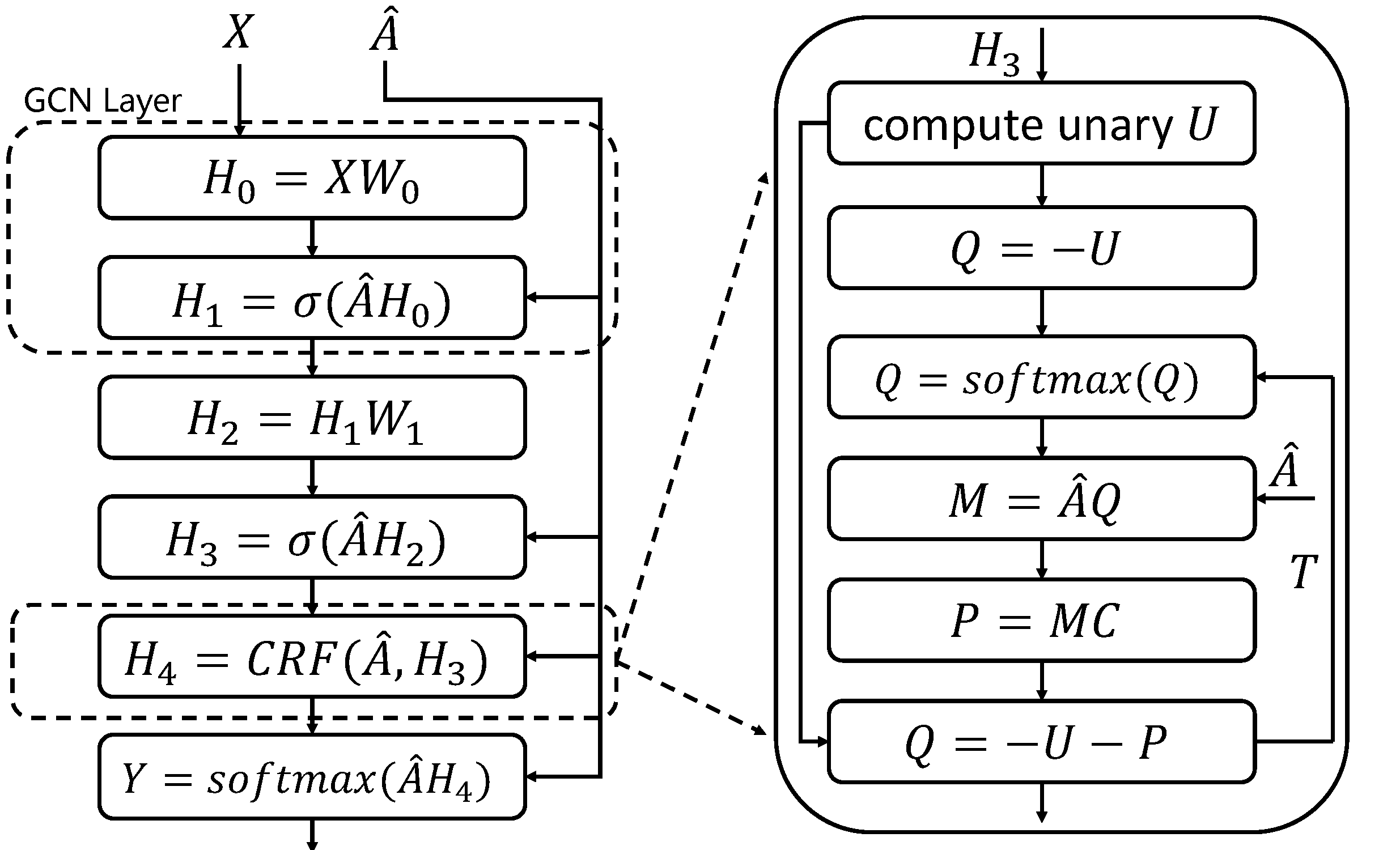

在CRF模块前，是拥有两层图卷积的GCN。第一个GCN层用来做特征编码，其中$X \in \mathbb{R}^{N \times d}$为节点的输入特征，$W_0 \in \mathbb{R}^{d \times h}$ 将原始输入的$d$维特征映射到$h$维的编码空间，用矩阵$A \in \mathbb{R}^{N \times N}$对感受野（一阶邻居）内节点的特征进行加权求和（卷积过程），$\sigma$为非线性激活函数，比如ReLu函数、Sigmoid函数和tanh函数等，本文采用了ReLu函数。紧接着第一个GCN层，第二个GCN层使用$W_1 \in \mathbb{R}^{h \times c}$对编码特征$H_1$进行分类，当然这里的分类结果$H_3$为未使用softmax函数进行归一化处理时的中间结果。GCN-CRF的目的就是在GCN后面的softmax层之前添加CRF模块来平滑GCN的分类结果。由于Zheng^{zheng2015conditional}将CRF表述为RNN模块，本文便可以很方便直接将该CRF模块加载在GCN后面，构建出一个端到端的深度神经网络模型，并采用标准的反向传播来训练模型，同时调整CRF和GCN中参数。值得注意的是，CRF中只有一个参数$\alpha$，这大大减轻了模型的训练难度。图中的CRF模块是基于算法 1 设计的，CRF中的能量函数的定义参照公式(1)和公式(4)。接下来，本文结合算法1 具体解释GCN-CRF模型结构图中的CRF模块。

首先需要计算一元能量$U$，由于GCN的输出为类别的概率分布，本文采用PyDenseCRF中的方法将类别概率分布转化为能量$U$，对应CRF模块中的第一层。CRF模块中的第二、三层对应于算法1中的$Q$的初始化，紧接着$ M = \widehat{A}Q $ 对应于消息传播过程。$P = MC $ 对应兼容性转换，其中 $C \in \mathbb{R}^{c \times c}$ 为兼容性矩阵，其定义为：

$$C_{ij} = \begin{cases} 1 & \quad \text{if } i \neq j \quad \\ 0 & \quad \text{if } i=j \end{cases} \tag{5}$$

对角为0表示一条边上的两个节点如果取相同的标签就不引入误差，否则给出惩罚，这里惩罚都取1。$Q = -U -P$ 对应算法1循环中的第三步，最后再归一化$Q$进入循环。Krähenbühl^{krahenbuhl2011efficient}指出，其提出的平均场推理算法在求解全连接CRF时一般在10次迭代内收敛（CRF模块中的$T$）。在本章提出的GCN-CRF模型中，处理的图是稀疏的而且实验表明5次迭代就已经足够，增加迭代次数并不会提升分类性能。

参数估计

本文采用了GCN^kipf2016semi的思想，使用神经网络模型$f(X,A)$直接对图结构进行编码，并在有监督损失$\mathcal{L}_{label}$上进行训练，从而避免了在损失函数中显式的添加基于图的正则化。使函数$f(\cdot)$条件于图的邻接矩阵将允许模型从有监督损失$\mathcal{L}_{label}$中分配梯度信息，并且使模型同时学习具备和不具备标签的节点的特征表示。具体地，对于半监督节点多分类问题，损失函数为定义在所有标记样本上的交叉熵。交叉熵用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小，一般用来做为神经网络的损失函数，其形式为：

$$\mathcal{L} = \sum_{i \in V^L} \sum_{j=1}^C Y_{ij} \ln \frac{1}{ \widehat{Y}\_{ij} } = - \sum_{i \in V^L} \sum_{j=1}^C Y_{ij} \ln \widehat{Y}\_{ij} \tag{6}$$

其中$V^L$为标记节点集合，$C$为类别个数，$\widehat{Y}$为推理的类别标签，$Y$为从数据集中获得的真实标签。由于从数据集中获得类别标签$Y$一般是硬编码的，也就是在类别上的one-hot编码，并且在一个类别上为1，在剩余的类别上为0。比如节点$vi$的真实类别为$k$，那么$Y{ik} = 1$， 并且在剩余的类别上$Y{ij} = 0$。 根据交叉熵的定义，对于节点$v_i$，只会在$k$这一类上计算损失，因为其他的$Y{ij} = 0$。 那么最小化损失函数将导致推理结果在第$k$类上尽可能大，即使$\widehat{Y}_{ik}$足够大，对其他类别没有约束。

对于模型的训练，本文采用了全批次随机梯度算法，每次输入全部样本进行训练。为了减轻存储的开销和加速计算，本文使用了稀疏矩阵来表示邻接矩阵$A$，使其内存需求变为$\mathcal{O}(|\mathcal{E}|)$，也就是与图中边的数目成线性关系。实验结构将在后文统一给出。

参考文献
^{zheng2015conditional}: ZHENG S, JAYASUMANA S, ROMERA-PAREDES B, et al., 2015. Conditional random fields as recurrent neural networks[C]//Proceedings of the IEEE International Conference on Computer Vision. 1529–1537.
^{fulkerson2009class}: FULKERSON B, VEDALDI A, SOATTO S, 2009. Class segmentation and object localization with uperpixel neighborhoods[C]//Computer Vision, 2009 IEEE 12th International Conference on. IEEE: 670–677.
^{chen2016deeplab}: CHEN L C, PAPANDREOU G, KOKKINOS I, et al., 2016. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs[J]. arXiv preprint arXiv:1606.00915.
^{krahenbuhl2011efficient}: KRÄHENBÜHL P, KOLTUN V, 2011. Efficient inference in fully connected crfs with gaussian edge potentials[C]//Advances in neural information processing systems. 109–117.
^kipf2016semi: KIPF T N, WELLING M, 2016. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907.