高阶依赖建模一直是图编码研究的热门话题，通过高阶依赖建模能捕获更长的网络结构依赖，保持节点之间的高阶近似。直观上，两个节点没有边相连，并不意味着这两个节点不相似。相反，如果两个节点在网络上通过某些节点能建立很强的联系，这两个节点仍然可以被认为相似。上一章提出的GCN-CRF模型，是基于GCN做图编码的。但是GCN是基于图上谱卷积的一阶近似方法，从而只能捕获一阶依赖。本章的目标是对更远的依赖范围进行建模。接下来的部分将具体给出针对高阶依赖进行建模的思考与建模过程。

高阶依赖建模

本文认为不同节点之间的$k$阶关系信息（对于不同的$k$值）揭示了与该图相关的有用的全局结构信息，并且在学习一个良好的图表示时，显式充分利用这一点非常重要。 下图给出了一些说明性的例子^{cao2015grarep}，展示了对于节点$A_1$和$A_2$，需要捕获$k$阶（对于$k=2,3,4$）关系的重要性。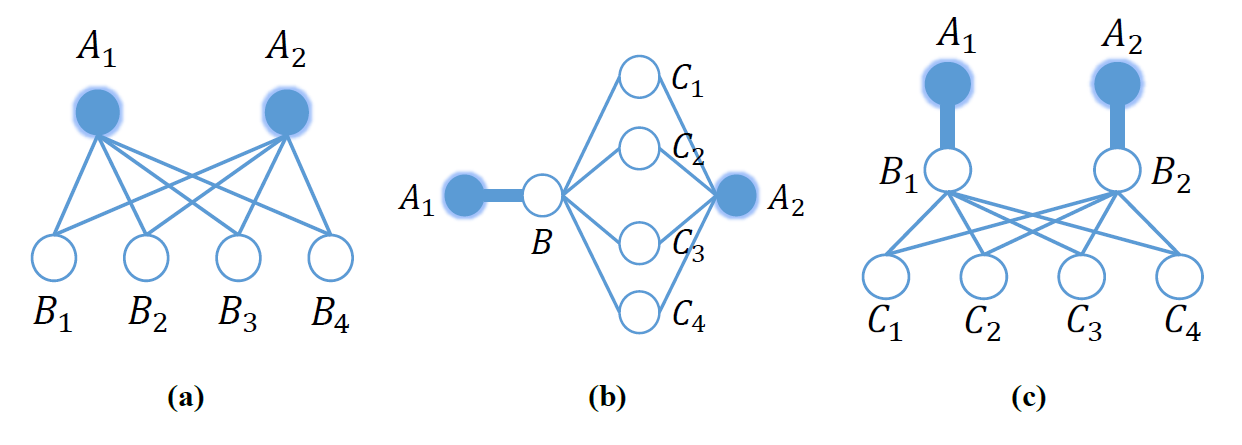

在该图中，粗线表示两个顶点之间的强关系，而细线表示较弱的关系。图a)示意了2阶信息，其中节点$A_1$和节点$A_2$没有直接相连，但是共享了很多邻居。显然，两阶信息对于捕捉两个节点之间的连接强度是非常重要的，它们共享的邻居越多，它们之间的关系也就越强。图b)展示了3阶邻居信息。节点$B$和节点$A_2$之间的大量共同邻居，增强了节点$A_1$和节点$A_2$之间的联系。图c)描述了4阶邻居的情况。从节点$A_1$到节点$A_2$需要走4步，但是$A_1$和$A_2$分别与$B_1$和$B_2$有很强的连接关系而且$B_1$和$B_2$共享了4个邻居，这使得$A_1$和$A_2$之间的关系很明显是很强的。显然，为了利用全局结构信息学得更好的图表达，高阶依赖的信息必不可少。

图中的高阶近似度量一般可以表示为非对称的概率转移矩阵$S$，反映节点之间的相关程度。一种直观的方式便是学习得到该概率转移矩阵，然后用该矩阵$S$替代上一篇文章中分类任务的邻接矩阵$A$。常见的概率转移矩阵$S$的计算方式有：Katz Index、Rooted PageRank、Common Neighbors和Adamic-Adar等。以上高阶近似的度量方式虽然简单，但是需要计算两个大矩阵之间的乘法，当网络中的节点数目$N$较大时，时间和空间的开销都较大。因此，本文并没有采用以上方式来对高阶依赖进行建模。受CLN（Column Network）^{pham2017column}的启发，本文采用多个隐层堆叠的方式来对高阶依赖建模。下图展示了CLN是如何通过堆叠多个隐层来捕获高阶依赖的：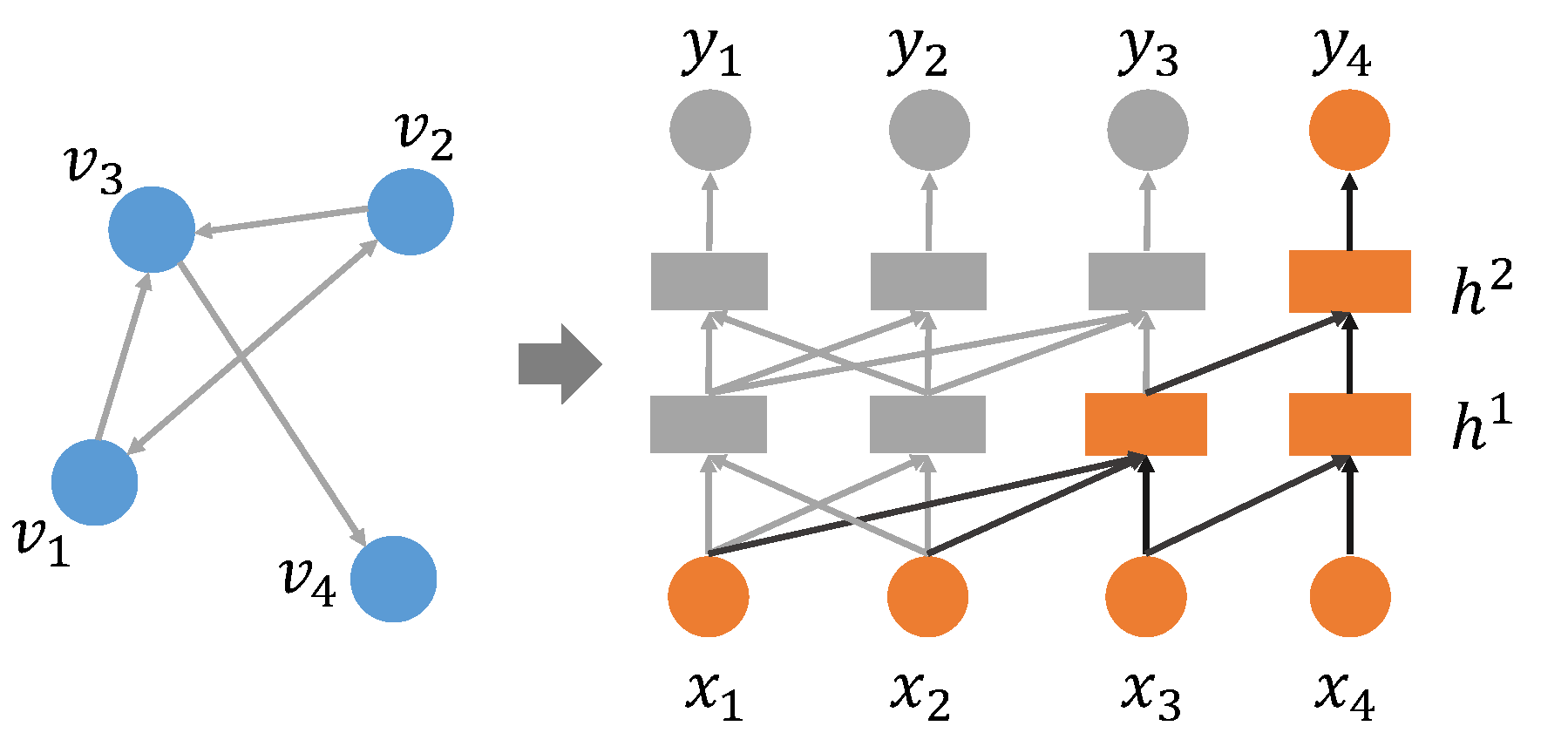

在图中，左侧是一个简单的拥有4个节点的图结构，右侧是其对应的CLN模型。CLN根据邻接矩阵$A$来对构建层与层之间的连接关系。图中高亮了推理节点$v_4$的过程。这里的示意图有两个隐层，因此能捕获二阶依赖。从推理结果$y_4$反向看过来，首先 $y_4$ 是基于隐层 $ h_4^2 $（编码结果）通过分类器得到的，而 $ h_4^2$ 通过邻接矩阵$A$接受前一个隐层的输入 $ h_3^1 $ 和其本身 $h_4^1$ 。该过程为通过邻接矩阵$A$捕获的一阶依赖。通过两个隐层的堆叠，最终$y_4$的计算依赖于图中所有节点：$ x_1 $ 到 $ x_4 $ ，因此隐式捕获了二阶依赖。 堆叠更多的隐层将会捕获更高阶的依赖关系。

Graph-GRU

模型结构与解释

然而，CLN本质上仍是全连接的前馈神经网络，只是根据邻接矩阵舍弃了一些连接，因此隐层的数目不能太多，太多不利于梯度的反向传播，造成梯度消失或者梯度爆炸。从CLN中不难发现，从节点特征$X$到推理结果$y4$的过程可以视为四个前向序列。循环神经网络（Recurrent Neural Networks, RNN）为一种常用的处理序列数据的方案，最常使用的RNN模型为LSTM（Long-Short-Term-Memories）模型。为了捕获长距离依赖，LSTM引入门（Gate）的机制来解决序列过长造成的梯度爆炸和梯度消失问题。 LSTM的单元模块中有三个门：遗忘门$f_t$、输入门$i_t$和输出门$o_t$。遗忘门$f_t$控制忘记多少上一时刻的单元状态$c{t-1}$，并将剩余的信息累积到当前时刻的单元状态$c_{t}$中。输入门$i_t$控制当前时刻的信息有多少可以融入cell状态$c_t$中。输出门$o_t$控制当前时刻的单元状态$c_t$有哪些信息需要输出到当前时刻隐状态$h_t$。LSTM中最核心的是单元状态$c_t$。$c_t$ 像一个传送带，直接打通整个LSTM序列。在整个前向传播的过程中只在$c_t$上进行一些简单的线性操作，通过门来控制$c_t$中信息的增减，这使得信息可以沿着它以不变的方式流过序列。由于是线性操作，在反向求梯度的时候，将一般多层前馈求梯度中的乘法变成了加减法，从而解决累乘造成的梯度爆炸和消失问题。

RNN一般用于语音、词序列和时间序列等一维的序列结构，但是本文现在要处理的问题是二维的网络结构，两者的共同之处是，本文同样需要学习长的邻居依赖。这个模型的迁移就是本章工作的要点。近期，Liang^{liang2016semantic}提出了Graph LSTM，扩展传统的LSTM模型，使其可以应用在图结构的数据上。Graph LSTM通过以语义上的超像素为节点，节点之间的空间邻近关系作为边，构建无向图。与传统LSTM向固定的序列邻居结构传递消息不同的是，Graph LSTM的每个超像素节点向图结构上的其他邻近超像素节点传递消息，不同节点的邻居结构是不同的。在节点的信息更新上，首先通过自适应的方式选出一个开始节点，然后按照信心驱动方案（Confidence-driven Scheme）来确定更新序列。这样确实是一种常规的方案，但是在模型的训练过程中需要提前训练好前面的CNN层，然后再更新LSTM节点，最后用梯度下降来调整参数。虽然是端到端的模型，但是需要两次训练，而且更新LSTM节点的过程，不仅在实现上比较麻烦，而且计算过程也会比较费时。因为必须按顺序更新，不是一个同步的过程。借鉴于LSTM的思想，本章提出了另外一种在图结构上实施RNN的方案。为了进一步减少模型参数，本文采用了LSTM的一种变体GRU（Gated Recurrent Units）^{Cho2014Learning}作为基本单元模块，并提出了图门控循环单元模型，Graph-GRU（Graph Gated Recurrent Units），采用RNN来保持$k$阶近似。

如果把构建的二维无向图平放在一个平面上，Graph LSTM方案可以说是在水平方向上构建RNN模型。那么本章提出的Graph-GRU可以视为在“竖直”方向构建RNN，通过复制构建的图使得每个隐层代表一个图，隐层与隐层之间通过邻接矩阵$A$构建连接，就像CLN那样。与CLN不同的是，Graph-GRU将隐层中的每个节点替换成了RNN单元，在隐层之间构建GRU，从而解决梯度爆炸和梯度消失的问题。这使得Graph-GRU将RNN变成在隐层之间的前馈过程，并能构建更深的模型，捕获更长范围的依赖，构建保持更高阶近似的模型。结构如下图：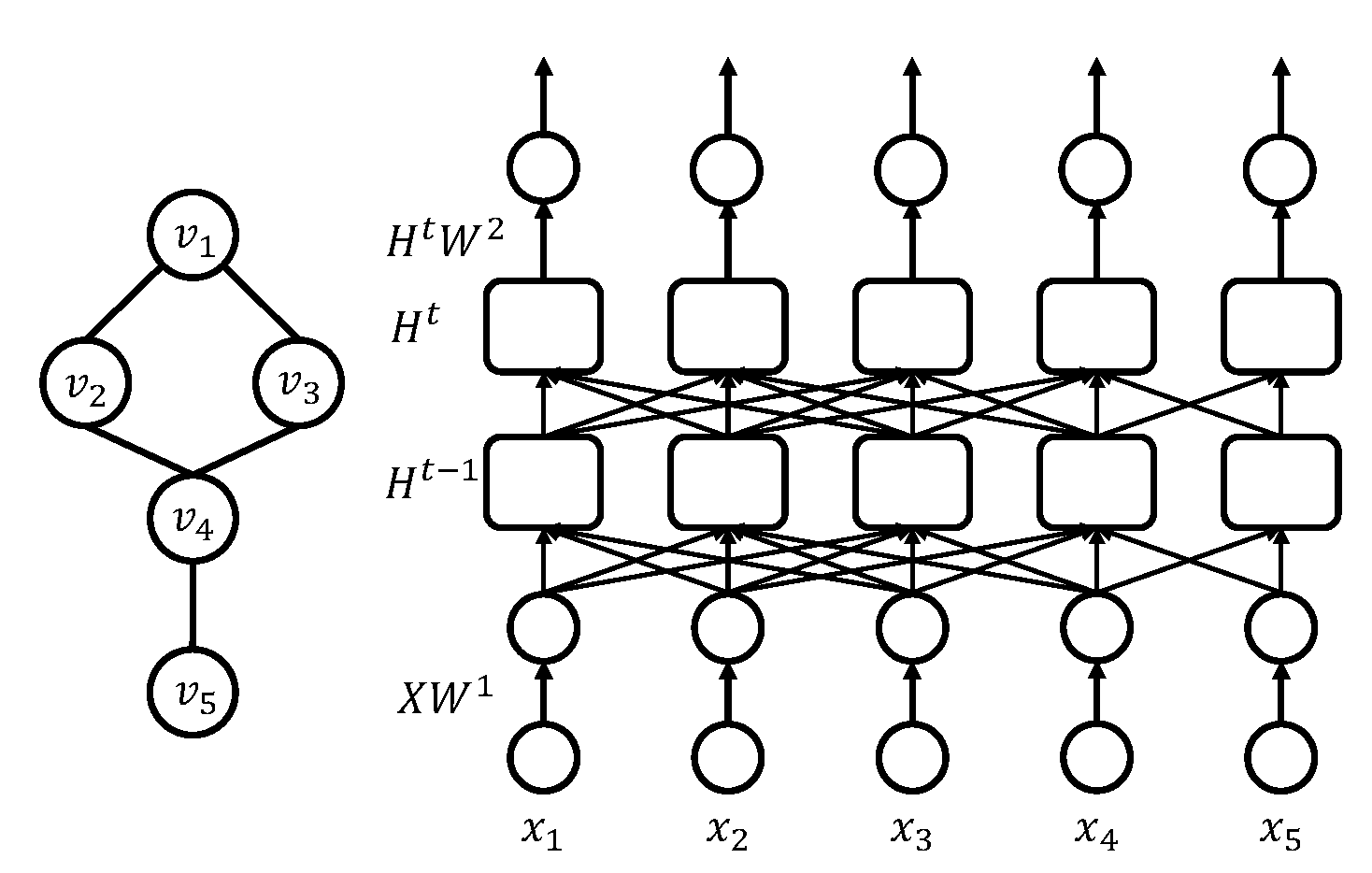

假设有一个包含5个节点的无向图，如图中左边部分所示，其对应的Graph-GRU模型的模型结构见图中右边部分。图中矩形框为GRU单元，一个GRU单元代表网络中的一个节点。该单元可以视为一系列运算的集合，只是这些运算在不同节点上重复出现，因此将其模块化来简化求解。可以看到，每一层有5个节点，代表左边无向图中的5个节点，层与层之间的连接反映了左边无向图的图结构。通过构建多层网络，最后输出层的每个节点可以捕获多步邻居的依赖，这个具体已经在上一小节中给出了解释。当然，随着层数的增多，会使模型变复杂，训练更费时，求解更困难。通过实验分析，本文最终选择的隐层层数为5-6层。

按照上一篇文章中的公式定义，$X \in \mathbb{R}^{N \times d}$为输入特征矩阵，$W^1 \in \mathbb{R}^{d \times h}$ 和 $W^2 \in \mathbb{R}^{h \times c}$为可以训练的隐层权重矩阵，其中$N$为网络中节点个数，$d$为输入特征维度，$h$为编码空间的维度，$c$为类别个数。$H^i \in \mathbb{R}^{N \times h}$ 为第$i$个隐层的输出。在Graph-GRU中，输入特征首先被映射到一个$h$维的隐空间：

$$H^0 = \sigma (XW^1)$$

其中$\sigma$为非线性激活函数，本文选用ReLu激活函数。接下来，信息在隐层之间传播。隐藏层之间的连接由图结构（邻接矩阵$A$）引导。 也就是说，如果图中节点 $ v_i $ 与 $ v_j $ 有边相连，第$t-1$个隐层中的第$i$个节点 $h_i^{t-1}$ 将连接下一隐层的第$j$个节点 $ h_j^t $ 。

为了区分不同结构的邻居，本文采用了GCN中的处理技巧，使用再归一化后的图拉普拉斯矩阵$\widehat{A} $来作为图中边的连接权重。同时，节点$ h_i^{t-1} $也与节点 $ h_i^t $ 相连，来获取节点 $ v_i $ 自身在前一个隐层的输出。因为隐层之间为RNN的连接关系，$ h^t $ 便对应了RNN单元的单元输出。通过多个隐层的编码，最后一个隐层 $ H^t $ 的输出即为保持了高阶近似的图节点编码结果。基于该编码结果，最后连接一个softmax分类器来输出模型的分类结果 $ Y \in \mathbb{R}^{N \times c} $ ：

$$Y = \text{softmax} (H^t W^2)$$

RNN模块

接下来，本节对Graph-GRU中的RNN单元进行介绍，并解释信息是如何在隐层间前向传播的。首先需要注意的是，标准GRU单元模块有两个输入，当前时刻的输入特征$x_t$和前一时刻的隐状态$h_t$。但是，在本文处理的问题中，每个节点有多个邻居的输入和其自身的前一时刻的状态输入。为了弥补这一差异，本文将标准的GRU单元进行了一定的修改，将汇聚了邻居信息的$g^{t}$作为输入特征$x_t$并将上一个隐层的输出作为$h_t$。下描述了使用的RNN单元的内部结构。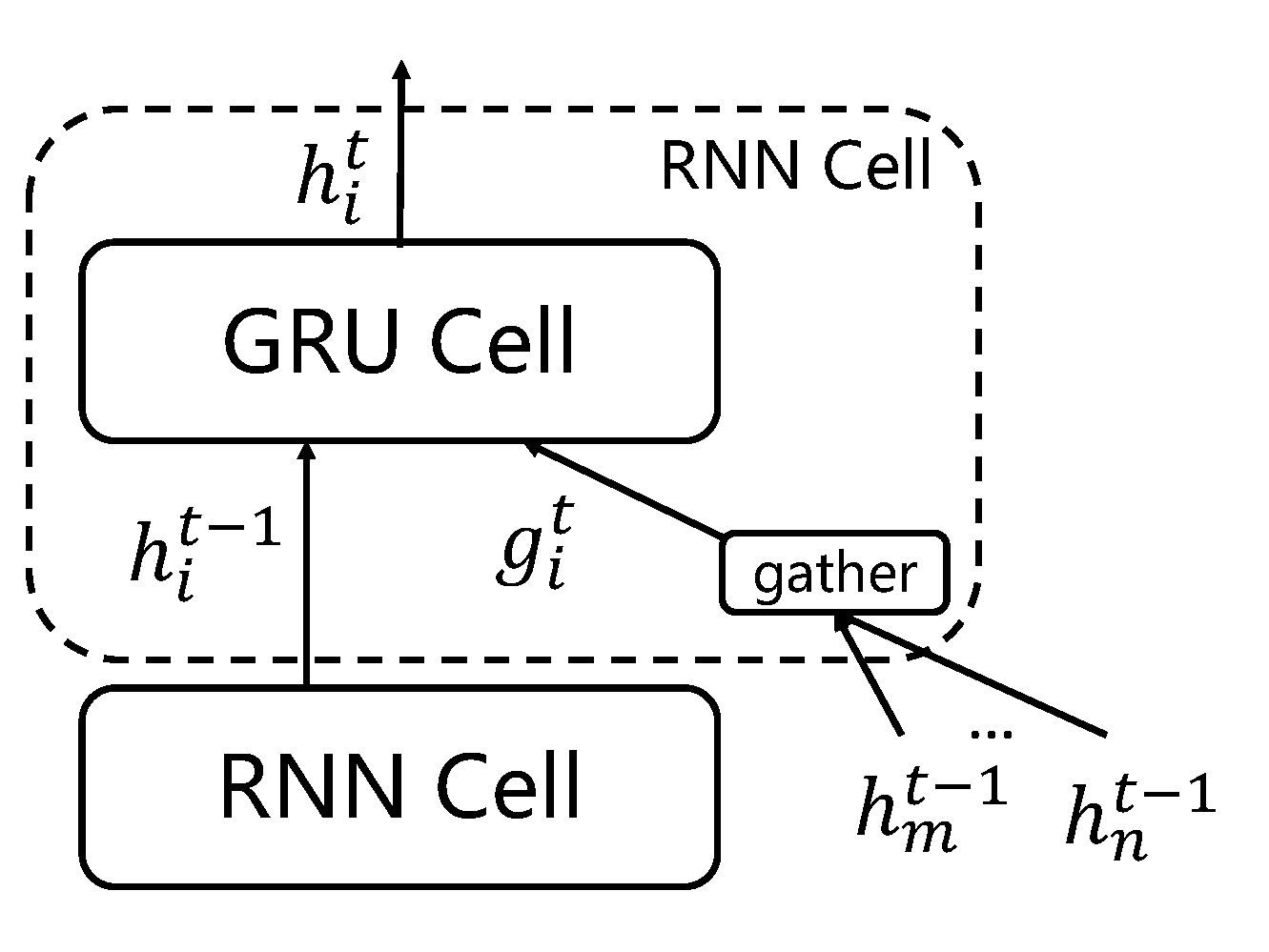

图示的RNN单元为第$t$个隐层的第$i$个RNN单元，对应于图中的节点$v_i$。该单元首先会接收节点$v_i$的上一个隐层的输出$ h^{t-1}_i $ ，这个过程与标准的GRU模型保持一致。不同的是GRU单元中的当前时刻的特征输入$x_t$，本文的GRU层是纵向前馈的，而且需要汇聚邻居的信息。在GCN中，节点汇聚了邻居的信息后，结合自己的旧信息，加权求和得到了自己的新信息。所以加权求和后的邻居信息一定程度反映了目标节点的信息，加权求和后的邻居信息也可以视为目标节点的上下文，故可以作为当前时刻的特征输入。于是，本文将$g^{t}$定义为：

$$g_i^t = \sum_{j \in N(i) } a_{ij} h_j^{t-1}$$

其中$N(i)$为节点$vi$的邻居集合，$a{ij}$为节点$v_i$与节点$v_j$之间边的权重。这里本文采用GCN中计算方式：

$$\widehat{A} = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$$

使用$a{ij} = \tilde{A}\{ij}$来度量节点间的相似性。上图中$h_m^{t-1}$和$h_n^{t-1}$示意节点$v_i$的邻居。与节点 $ h_i^{t-1} $ 一样，$ h_m^{t-1} $和$ h_n^{t-1} $也是RNN单元的输出，这里为了简洁起见，省略了它们的单元框。

得到了$ g^t $ 后，$ g^t $ 连同 $h_i^{t-1}$ 一起被送入GRU单元。在GRU单元中有两个门，重置门 $r^t$ 和更新门 $z^t $，其计算方式为：

$$r^t_i = \sigma (W^r g^t_i + U^r h^{t-1}_i)$$ $$z^t_i = \sigma (W^z g^t_i + U^z h^{t-1}_i)$$

其中$W^r, U^r, W^z, U^z \in \mathbb{R}^{h \times h}$ 为各个门的可以训练的权重矩阵。这些权重在所有RNN单元上共享，增加GRU隐层不会增加模型参数。得到两个门后， 首先通过重置门 $r^t$ 来控制当前时刻需要保留多少上一时刻的信息，并得到候选隐状态 $\widetilde{h}^t$ ，等待输出。

$$\widetilde{h}^t_i = \text{tanh}(g^t_i +r^t_i h^{t-1}_i)$$

注意这里的计算与标准的GRU不同，如果按照原本的GRU，其计算方式为$\widetilde{h}^t_i = \text{tanh}(Wg^t_i +r^t_i U h^{t-1}_i)$ 。 此处，本文省略了权重矩阵$W$和$U$来减少模型的参数。事实上，实验表明，这样的处理能提升推理正确率。 其次更新门 $ z_i^t $ 选择性地遗忘前一时刻的隐状态$h^{t-1}_i$，并加入当前时刻的隐状态信息，得到最终的输出 $h_i^t$ ：

$$h^t_i = z^t_i \circ h_i^{t-1} + (1-z^t_i) \circ \widetilde{h}^t_i$$

这里$\circ$为按位乘运算。由于$W$和$U$都是$h \times h$ 的矩阵，得到的门 $ r_i^t $ 与 $ z_i^t $ 均为$h$维的向量。也就是说，在特征的每个维度上都有个权重，控制每个维度信息的通过。

模型训练

Graph-GRU损失函数的定义与GCN-CRF的定义一致，本章不再赘述。对于模型的训练，本节更加关注的是模型的训练方式：Full Batch和Mini-batch。

Full Batch

Full Batch方式，顾名思义，每次进行训练时输入全部的训练样本，在全部样本上计算损失函数，然后针对每个参数计算梯度。全批次方式一般用于数据量较少的情况，由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向 。数据量较大时，输入全部样本会造成内存开销太大和训练时间长等问题。但是，在图结构数据上，采用全批次方式似乎是最优的方法。由于图的整体结构的约束，去除任何样本，或者任何对样本的划分方式，都会造成网络结构的不完整，影响推理的准确性。因此目前基本所有图编码方法都是采用的全批次方式，上一章描述的GCN-CRF也是采用全批次方式进行训练的。

上文所示的GRU模型结构示意图就是全批次方式。由所有样本的特征组成的特征矩阵$X$被用作输入，通过Graph-GRU学得所有样本的类别标签$Y$。然后，部分节点（有标记的节点）的输出$y_i$会反向传播有监督损失，剩余节点保持不动。由于网络的连接，反向的梯度能传到网络中未标记节点。

Mini-batch

在Mini-batch方式中，每次挑选一部分（batch大小）样本用作训练，而不是全部数据，通过多次分批多次调整模型参数。如此一来，每次参与训练的数据量可以调控，不至于太大导致内存不够用，减少计算量，提高内存利用率。同时每次挑选一批样本而不是一个样本，可以减少梯度下降的随机性。因此小批次方式在大样本情况下得到了广泛的应用。
值得注意的是，全批次和小批次方式一般都用于有监督学习，在半监督模型上采用小批次将会面临如何挑选合适的有标记和无标记样本的难题。倒是全批次方式不必担心这个问题，因为它将所有样本都用于了训练。根据上文所述，任何数据子集的选取方式都会造成网络的完整，故基于图半监督学习的小批次方式的构建是一个很有挑战和意义的问题。

针对以上问题，本文给出了一种简单的小批次训练方式。对于每个batch，首先挑选一个目标节点集合（该batch的种子样本），这些节点最好是从一个社区或者紧密连接的节点群体中挑选。然后，所有种子节点的$k$阶邻居（这里$k$对应于Graph-GRU中隐层的数目）被挑选入当前batch的训练集合，并由这些节点构建一个局部子图。极端情况下，可以将整个网络中的每一个联通子图作为一个batch。
这样的挑选方式将使每个节点在模型中的计算方式（具体指依赖的$k$阶邻居）与全批次方式一致，同时也减少了每次参与训练的节点数目。最后在构建的子图上训练模型。不难看出，相同的节点可能出现在不同的batch中，那么节点的类别标签推理结果可以有两种方式确定：其一，对每个batch中的推理结果求平均、取最大或者投票的方式。其二，小批次只是用来调整模型中的参数，小批次训练结束后，将所有节点喂入模型，只计算前向过程，预测得到所有样本的类别标签。

参考文献

^{cao2015grarep}. CAO S, LU W, XU Q, 2015. Grarep: Learning graph representations with global structural information[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. [S.l.]: ACM: 891–900. ↩

^{pham2017column}. PHAM T, TRAN T, PHUNG D Q, et al., 2017. Column networks for collective classification.[C]//AAAI. [S.l.: s.n.]: 2485–2491. ↩

^{liang2016semantic}. LIANG X, SHEN X, FENG J, et al., 2016. Semantic object parsing with graph lstm[C]//European Conference on Computer Vision. [S.l.]: Springer: 125–143. ↩

^{Cho2014Learning}. CHO K, VAN MERRIËNBOER B, GULCEHRE C, et al., 2014. Learning phrase representations using rnn encoder-decoder for statistical machine translation[J]. arXiv preprint arXiv:1406.1078. ↩