上一篇文章已经详细描述了在半监督图编码任务中，保持高阶近似的重要性。尤其当图比较稀疏时，节点的一阶和二阶邻居的数目太少以致于不能准确反映节点的上下文。从更细的角度来看，图中不同节点所处的位置不同，其局部图结构也就不同。有些节点处于图中比较稠密的部分，比如社团中部，邻居信息足够，能准确地反映节点的类别分布。但是信息过多也不一定是一件好事，比如有些节点夹在两类节点和两个社团的中间，这些节点的邻居很多但是信息也很杂，此时需要进一步扩大邻居范围，看其偏向哪一方。同时，也有一些节点处于一条长链的局部结构中，这些节点只有一个或两个邻居，就算扩大视野到2步邻居，信息也不够。在这种情况下，需要扩大感受野到整条链甚至到这条链所连接的社团。

上述描述是为了说明不同位置的节点需要的感受野大小不同（$k$阶邻居的$k$不同）。目前的模型包括之前提出的Graph-GRU都是对所有节点一视同仁，使得每个节点都捕获相同的$k$阶近似。显然，对于有些节点，这个固定的$k$值可能比较小，邻居信息不够；对于有些节点，$k$值可能稍微偏大，邻居信息太多以致于紊乱。因此，本章的出发点是，能否对不同节点自适应的捕获不同的高阶近似？此外，当捕获的$k$阶近似中$k$较大时，编码过程需要在以目标节点为中心的$k$阶子图上对目标节点的编码进行平滑。 此时，学得的编码可能过于平滑以致于丢失局部细节。基于以上出发点，本章提出了一个端到端的自适应高阶图编码（Adaptive High-Order Graph Embedding, AHOGE）神经网络，在自适应地保持高阶近似的同时保留个体细节特征。

自适应高阶图编码模型

下图给出了在一个拥有五个节点的简单图下的AHOGE模型的结构示意图。受Column Networks^{pham2017column}的启发，AHOGE利用$k$个隐层的堆叠来扩展半径为$k$的邻居感受野以实现 远程依赖（高阶近似）。由于第$i$个隐层捕捉$i$阶近似，所以AHOGE将一阶近似层连接在其后面所有隐层上，使得后面的隐层在捕获$k$阶近似的时候能融入一阶近似的信息，以防止过于平滑的编码结果。通过交叉验证，本文选择AHOGE的隐层数目$k=7$。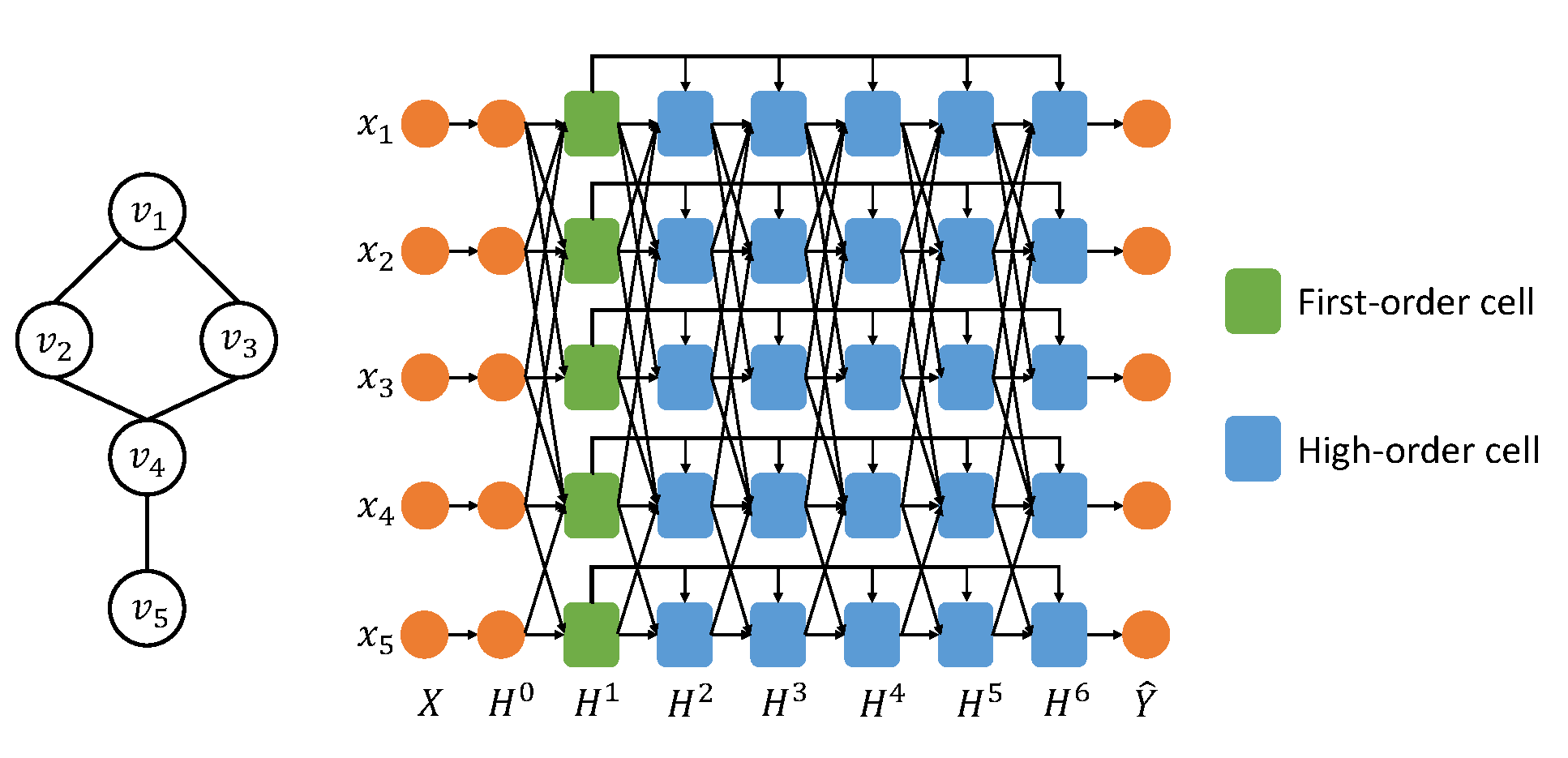

在AHOGE中，7个隐层有三种不同的类型，图中用不同的颜色区分开。具体为特征变换层、一阶近似层和高阶近似层。 $H^0$为神经网络中常见的特征变换层， $H^0 = \text{ReLU}(W^0X)$。$X \in \mathbb{R}^{N \times d} $ 为输入特征矩阵，其中$ N $为图中节点个数，$d$为节点特征的维度。 $ W^0 \in \mathbb{R}^{d \times h} $将节点的特征从$d$维降到$h$维。后续所有的隐层都是在该$h$维的特征空间中对节点的特征进行调整。 $ H^1 $ 为一阶近似层，层中一阶近似单元自适应地收集一阶邻居的信息。$ H^2 $到$ H^6 $为高阶近似层，层中高阶近似单元自适应地融合$k$阶邻居的信息。
为了减少模型参数和防止过拟合，本文采用了参数共享和高速网络^{srivastava2015highway}的思想。首先，模型中相同类型的隐层共享相同类型的参数。其次，隐层$H^1$通过使用高速网络的方式连接到后面的高阶近似层。由于高速网络的性质，一个门$ \alpha_g^k $ 部分开放，让$H^1$能突破层间隔的束缚在整个网络上传播：

$$h^k = \alpha_g^k \circ h^1 +(1-\alpha_g^k) \circ \widehat{h}^k$$

$\widehat{h}^k $ 为不使用高速网络时隐层 $ H^k $ 的输出。 请注意，本文对网络中的每个节点都定义了这样一类门，本文为了简洁起见省略了$\alpha _{g,i}^k $ 中的$i$，对此类门做一般性描述。 这里门$ \alpha _g^k $不是固定的，是根据$ H^1 $ 的输出和当前隐层$ H^k $ 的输入来共同决定的。并且门$ \alpha _g^k $也是一个$h$维的向量，也就是说在隐层特征的各个维度上各有一个属于$(0,1)$范围的值来控制信息的通过。当$k$较小时，也就是在高阶近似层的前几层，$ h^k $ 与 $ h^1 $ 的差异较小，因此可以减小门$ \alpha _g^k $，更多的让 $ h^k $ 的信息传递进来，捕获高阶近似。当$k$较大时，也就是高阶近似层的后面的一些层，$ h^k $ 可能已经在较大范围的邻居上过于平滑了，丢失了节点个体信息，因此与 $ h^1 $ 偏差较大。此时应该增大门 $ \alpha _g^k $ ，让之前的一阶邻近 $ h^1 $ 占据更多的主动权，将局部细节补充进来。由于门的计算是自适应的，AHOGE的建模方式使其能够自适应地捕获高阶近似，编码的结果既包含了局部细节又融入了全局结构。 接下来，本章具体对模型中的一阶近似单元和高阶近似单元的结构进行介绍。

近似单元内部结构

一阶近似单元

图卷积神经网络（GCN）提出了一个简单但是效果很好的分层前向传播规则，用于解决图半监督节点分类问题。Kipf^kipf2016semi给出了一个两层的GCN，其核心是图卷积运算：

$$H^{\(l+1\)} = \sigma ( \widehat{A} H^{\(l\)} W^{\(l\)})$$

其中$\widehat{A}$为再归一化后的图拉普拉斯矩阵。 AHOGE同样也采用了GCN中利用$\widehat{A}$来收集局部一阶邻近信息的思想。

此外，在保持一阶近似的基础上，AHOGE还能自适应地保留个体细节。 在一阶近似单元中，GRU中的重置门和更新门的思想被采纳，通过这两个门来自适应地融合个体细节特征和捕获的一阶近似。下图展示了一阶近似单元的内部结构。请注意，在AHOGE中只有一层一阶近似单元，图z只是给出了其一般形式。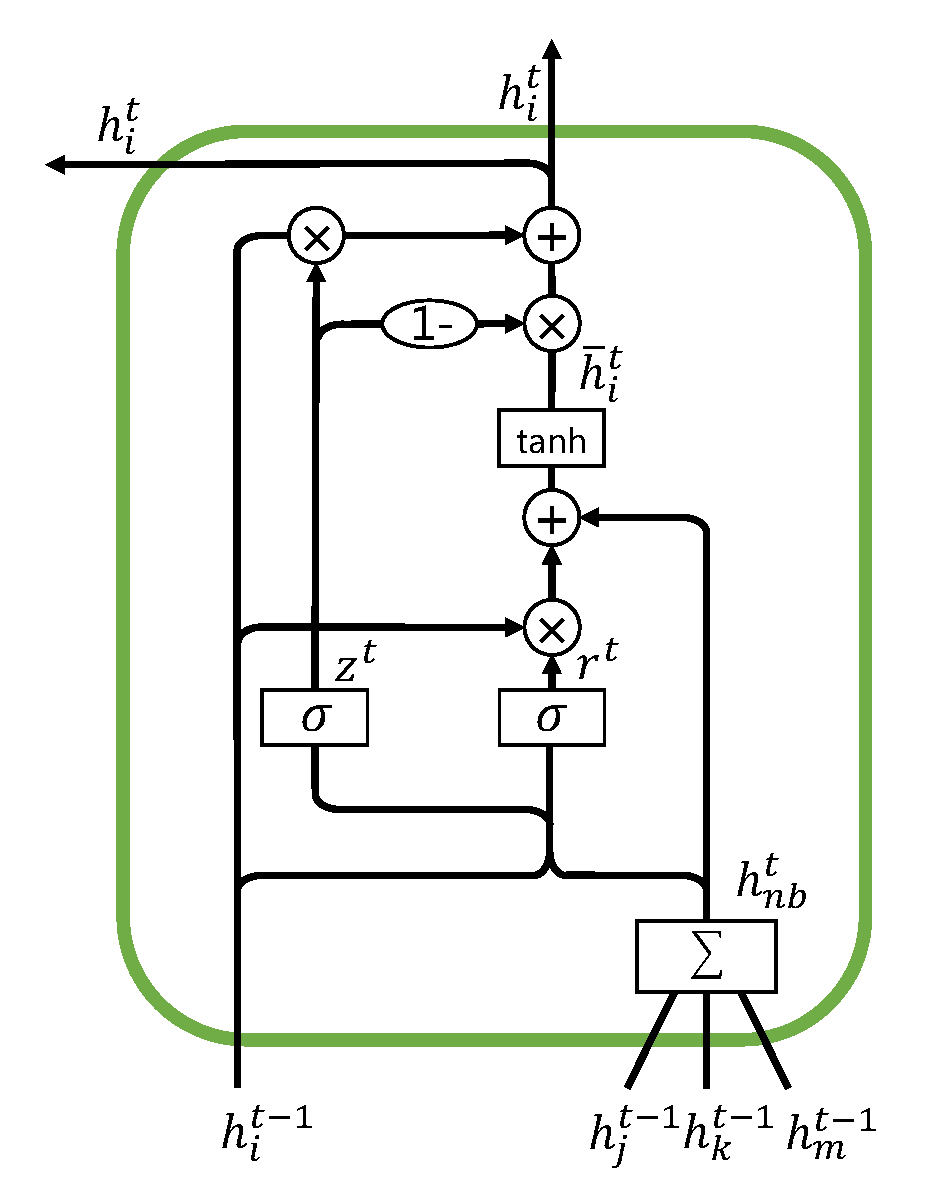

首先，该单元使用GCN中的技术收集一阶邻居的信息：

$$h_{nb,i}^t = \sum_{j \in N_i \cap i} \widehat{A}\_{ij} h_{j}^{t-1}$$

其中$Ni$为节点$v_i$的直接邻居的集合，$h_j^{t-1}$为第$t-1$个隐层中节点$v_j$的输出。在一阶近似中，$j$、$k$和$m$示意了节点$v_i$的邻居。 $ h{nb,i}^t $加权求和了节点$v_i$的一阶邻居，因此可以视为节点$v_i$在此时的上下文，保持了一阶近似。

其次，该单元使用重置门来控制前一隐层的输出$ h^{t-1} $中有多少信息需要被保留，并使用tanh激活函数做非线性变换得到预输出$ \overline{h}_i^t $。

$$r^t_i = \sigma (W^r h_i^{t-1} + U^r h_{nb,i}^t)$$ $$\overline{h}\_i^t = \text{tanh} \( h\_{nb,i}^t + r^t_i \circ h_i^{t-1} \)$$

$ W^r \in \mathbb{R}^{h \times h}$和$U^r \in \mathbb{R}^{h \times h} $为该重置门的可训练参数，控制每个维度上的权重。$\circ$为矩阵上的按位乘法。 $ \overline{h}_i^t $可以视为此一阶近似单元的隐状态。

最后，更新门$z^t$决定了需要遗忘多少上一层的信息，合并单元隐状态$ \overline{h} _i^t$ 得到最终的输出：

$$z^t\_i = \sigma (W^z h\_i^{t-1} + U^z h\_{nb,i}^t)$$ $$h\_i^t = z^t\_i \circ h\_i^{t-1} + (1-z^t_i) \circ \overline{h}\_i^t$$

$W^z \in \mathbb{R}^{h \times h}$和$U^z \in \mathbb{R}^{h \times h}$为该更新门的可训练参数。

在AHOGE中，此时的$ h^{t-1} $ 为 $ h^0 $ ，也就是输入特征经过特征变换层后的结果。$h^0$的计算尚未利用邻居的信息，因此可以认为 $h^0$ 保留了个体细节特征。 而$ h{nb,i}^t $利用$ \widehat{A}\{ij} $对邻居的 $h^0$ 加权求和，因此可以认为其捕获了一阶近似。不难发现，更新门和遗忘门从保留 $h^0$ 的信息以获取当前单元隐状态和遗忘$h^0$的信息得到最终输出两个角度，通过以 $h^0$ 和 $h_{nb,i}^t$ 作为输入自适应计算得到的各个维度的权重，来自适应地融合这两部分的信息。因此，一阶近似层$H^0$在保持一阶近似的同时自适应地保留了局部个体细节。

一阶近似单元有两个输出，将求得的 $h_i^t$ 分别传递到下一个隐层 $H^2$ 和各个高阶近似层 $H^k$ 。前者为神经网络中普通的前向传播，后者为采用高速网络的方式将隐层 $H^1$ 与后面的高阶近似层连接。后者的做法有两个目的：其一，将保留了个体细节的一阶近似通过高速网络自适应地合并入各个高阶近似中。其二，高速网络的提出是为了解决模型过深造成的梯度爆炸和梯度消息问题，AHOGE这样处理可以使得模型变得更深，捕获更高阶的信息，同时解决反向梯度求解的问题。

高阶近似单元

接下来，本节具体介绍高阶近似单元。下图说明了节点$v_i$对应的高阶近似单元的内部结构。该单元有三个输入：节点$v_i$自身上一层的输出$ h^{t-1}_i $、上一层邻居的输出$ h_j^{t-1} $和节点$v_i $在一阶近似层的输出$ h^1_i $。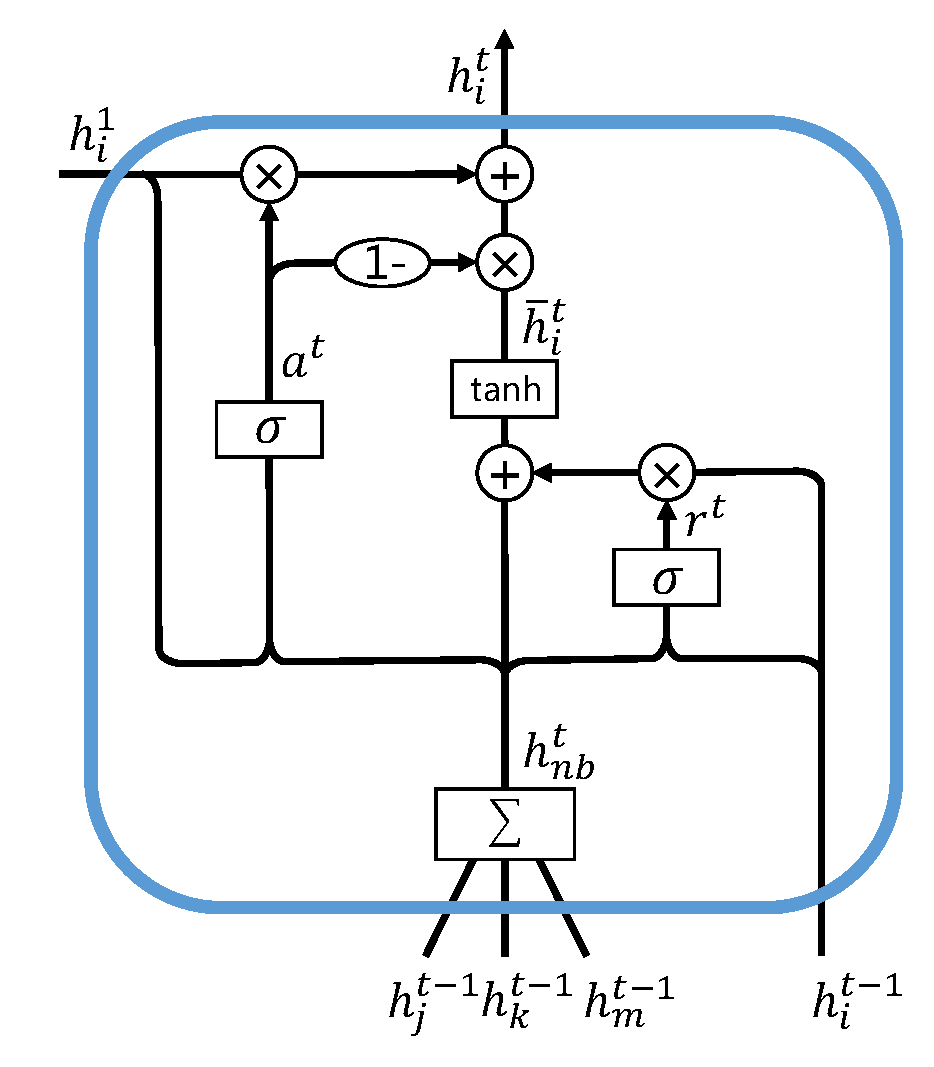

与上文的公式一致，此时的 $ h^t_{nb,i} $ 为一阶邻居的加权求和。高阶近似单元同样也有两个门：重置门和自适应门。重置门的定义与一阶近似单元中的一样，此处为了简练起见不再赘述。值得注意的是，一阶近似中两个门都是为了控制一阶近似和个体细节的信息的合并，这种定义方式是为了与GRU中的单元保持一致。但是，本文认为一个门就足够，具体的例子为高速网络。高速网络只使用一个门来控制两个输入的信息的合并。此处，为了减少模型参数，降低模型的复杂性，本文同样只采用一个门，也就是只使用重置门来控制节点 $vi$ 自身的输入 $h^t_i$ 和其上下文 $h^t\{nb,i}$ 。省下的更新门替换为自适应门，自适应门控制需要融合多少 $h_i^1$ 的信息。其定义为：

$$a^t_i = \sigma (W^a h_i^{1} + U^a h_{nb,i}^t)$$

在自适应门的影响下，高阶近似单元的输出$h^i_t $能自适应保留一阶近似 $ h_i^1$：

$$h_i^t = a^t_i \circ h_i^{1} + (1-a^t_i) \circ \overline{h}_i^t$$

根据上一章的描述，这种堆叠$k$个隐层的方式能使得第$k$个隐层的输出保持$k$阶近似。故该高阶近似单元的隐状态$\overline{h}_i^t$ 捕获了$k$阶近似。输出$h_t^i $在自适应保留一阶近似$ h_i^1 $信息的同时能保持高阶近似。而且，$h_i^1$在保持一阶近似的同时自适应保留了个体细节，所以AHOGE最后一个高阶近似层的输出 $h^6$（模型最终得出的图编码）能够自适应捕获高阶近似，并且自适应地融合了个体的细节特征。

在模型的最后是一个多分类softmax分类器，这里与GCN等大多数图编码方法一致。

^{pham2017column}. PHAM T, TRAN T, PHUNG D Q, et al., 2017. Column networks for collective classification.[C]//AAAI. 2485–2491. ↩

^{srivastava2015highway}. SRIVASTAVA R K, GREFF K, SCHMIDHUBER J, 2015. Highway networks[J]. arXiv preprint arXiv:1505.00387. ↩

^kipf2016semi. KIPF T N, WELLING M, 2016. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907. ↩