本文对上几篇文章说诉的方法进行了实验验证和总结。

数据集简介

本文使用了三个基准引用网络数据集：Cora、Citeseer和Pubmed^{sen2008collective}，在这三个数据集上验证所前几篇文章中模型的性能。 这三个引用网络数据集包括学术论文（视为图中的节点）和引用链接（视为图中的边）。下表总结了所用数据集的详细统计数据。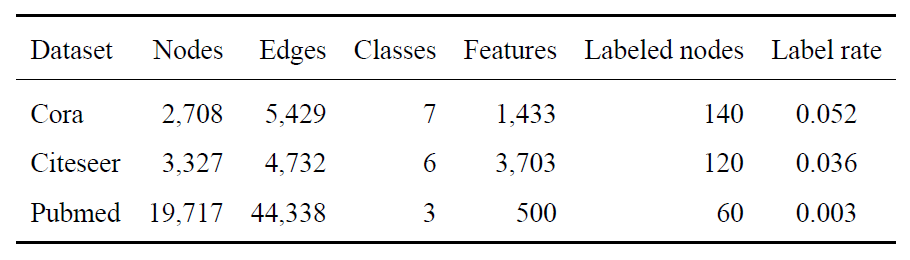

每篇论文（节点）都有一个稀疏的词袋表示的特征向量和一个专家标注的主题，这些主题来自一组预先定义好的类别。在Cora和Citeseer中，节点的特征向量中的元素为0或1的值，表示对应位置上的词是否出现在文档中。特征向量的维度即为词典的大小。在Pubmed中，每篇论文被描述为由500个词组成的词典计算的TF/IDF加权词向量。 与所有基线方法（baseline）一致，本文将由引用链接构建的图作为无向图，并将边权重设置为1。

如上表所示，本文首先按照Yang^{yang2016revisiting}的方式，固定训练集、验证集和测试集的划分方式，因为他们给出的划分方式是这些基准数据集的标准划分方法，已经被广泛采纳。在该划分方式中，每类有20个标记节点用于训练集，500个节点用于验证集，1000个节点用于测试集，其余节点都作为未标记节点。其中训练集、验证集和测试集的节点挑选是由Yang^{yang2016revisiting}固定给出的，故叫做固定数据集划分的实验部分。其次，为了验证模型的鲁棒性，本文同样采用了随机数据划分的方式，多次进行实验测试模型对标记样本位置的敏感性。

对比方法

本文将所提出的模型与Yang^{yang2016revisiting}和Kipf^kipf2016semi中描述的几种基线方法以及图卷积网络GCN^kipf2016semi进行对比。
其中有些方法在之前的章节中已经给了详细的解释，下面从利用的数据类型（网络结构 $ A $ 、节点特征 $ X $ 和节点类别标签 $ Y $）的角度将这些方法进行归类并做简单的介绍：

• 标签传播方法: LP（Label propagation）^zhu2003semi、ICA（Iterative classification algorithm）^lu2003link和ManiReg（Manifold regularization）^{belkin2006manifold} 在邻居之间传播标签信息，约束网络中边权重较大的两个节点的标签趋于一致，为非参数化的标签传播算法。ICA通过允许更一般的局部更新来扩展LP，ManiReg将LP中损失函数替换为SVM中的损失函数。这些方法只使用网络结构和节点的标签。
• 随机游走方法: DeepWalk^{perozzi2014deepwalk}和node2vec^{grover2016node2vec}为基于Skip-gram的图编码方法。这类方法通过随机游走生成节点的上下文，在此基础上利用Skip-gram学习图编码。这两个方法只利用网络结构来学习编码，忽略了节点的特征和标签。
• 半监督图编码方法: SemiEmb（Semi-supervised embedding）^{weston2012deep} 为最早使用神经网络的基于图拉普拉斯正则化的半监督图编码方法。这些方法在有标记样本上计算有监督损失，利用图拉普拉斯正则在所有样本上计算无监督损失。因此，模型训练过程中利用了网络结构、节点特征和节点标签三方面的信息。Planetoid^{yang2016revisiting} 同样利用了这三个方面的信息，该模型训练了一个编码来联合预测节点的类别标签和图上下文。GCN^kipf2016semi利用这三个方面的信息来构建一个统一的半监督图卷积神经网络模型，同时完成特征编码和节点分类任务。

实验结果

本文首先给出实验过程中的一些参数的设置。上文已经指出，训练集是在每个类别上挑选20个样本得到的。本文使用拥有500个样本的验证集来优化参数，比如dropout比率、L2正则项权重和学习率。训练好模型后，对于每个数据集，本文在1000个随机挑选的测试样本上评估预测的正确率。 在三个数据集上，一些共同的参数的设置如下：

• dropout： 0.5
• 学习率： 0.01
• 最大迭代次数： 200
• 编码特征维度： 16
• L2正则项权重：$ 5 \cdot 10^{-4}$

其中编码特征的维度，也就是隐层特征的维度，这里设置为16是为了与GCN中的设置一致。后文也会讨论编码特征的维度的影响。 虽然最大迭代次数为200，但是模型经常在此之前收敛。为此，本文采用early stopping来及时停止模型的迭代，并设置容忍的迭代次数为10，如果在10次迭代内模型的损失变化小于一定阈值就可认为已经收敛。

除了以上共同的超参数外，还有一些场景独立的超参数。对于GCN-CRF模型，本文设定其中CRF学习部分的迭代次数在所有数据集上都固定为5次。对于Graph-GRU模型，本文对Pubmed数据集使用4个GRU隐层，对于Cora和Citeseer 数据集使用5个GRU隐层。对于AHOGE模型，本文使用了1个一阶近似层和5个高阶近似层。

本文通过Tensorflow实现这些模型。所有的实验都是在仅有CPU的环境下进行的： 4-core Intel® Core™ i7-6500U CPU ® 2.5GHz

本节首先在固定数据集划分的情况下进行实验，分类结果总结在下表中。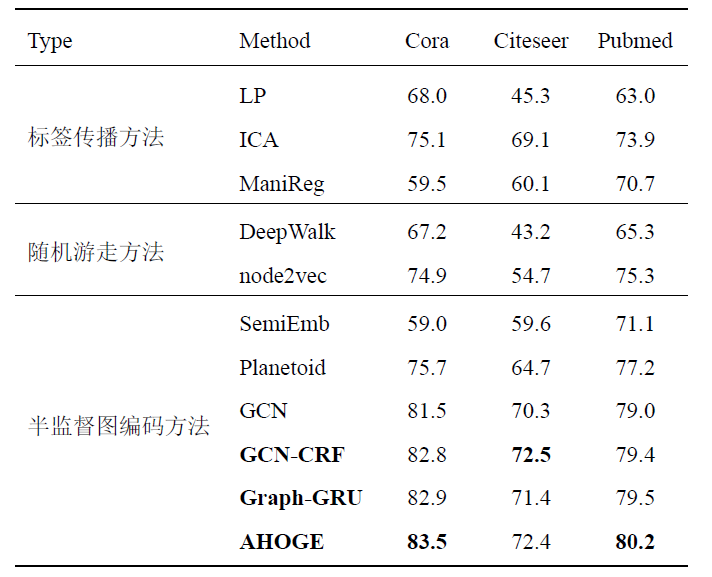

GCN-CRF在数据集Citeseer上取得了最好的结果，但是，相比于Graph-GRU在其他两个数据集上的正确率差不多。不难发现，数据集Citeseer的网络最为稀疏，为了获得较好的性能，Graph-GRU和AHOGE都堆叠多个隐层来获取充足的邻居信息。而GCN-CRF只有两个隐层，其主要发挥作用的是CRF模块。CRF模块对节点的分类结果添加约束，促使相邻且相似的节点分类结果趋于一致。事实证明，该CRF模块是有效的，尤其在稀疏网络结构上。

再看Graph-GRU和AHOGE，两者都能保持高阶近似，而且AHOGE可以视为是Graph-GRU的改进版，能在自适应地保持高阶近似的同时保留个体局部细节。AHOGE在三个数据集上的正确率均高于Graph-GRU，也证实了这一点。总体来说，AHOGE的性能最好，即使在稀疏的数据集Citeseer上，其分类正确率也与GCN-CRF接近。

固定数据集划分会造成一定的随机性，不一定能准确的反映模型的性能。因此，本文紧接着对数据集进行多次随机划分，用于观测模型在各方面的性能。

在该随机划分实验中，本文保持标记样本的数目不变，同样也是每类20个样本。同时，本次实验也保持验证集的大小不变，为500个样本。本次实验的一个目的是观察标记节点的在网络中的位置对模型推理结果的影响，因此本次实验固定测试集的样本不变，与上文固定数据集划分时的划分一致。这样做的目的就是在保持测试样本的位置不变的情况下，随机变动训练集和验证集样本的位置。还有一点与之前的方案不同，对于训练集与验证集的选取，本次实验不是为每个类选择20个样本，而是完全随机选择样本。 由于数据的类别标签的分布是不均匀的，这样随机选择训练样本可以保持分布结构。本次实验具体随机执行了20次不同的训练集和验证集的选取。

下表给出了20次随机数据集划分情况下的分类正确率和标准误。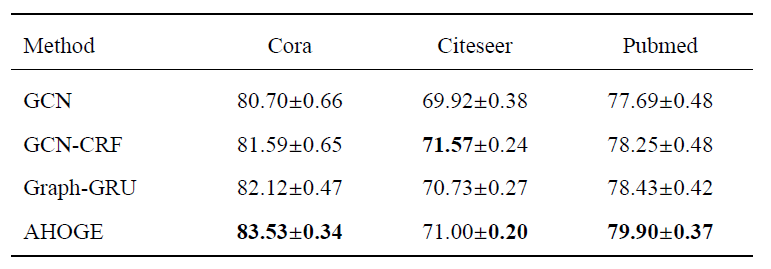

同样地，AHOGE在Cora和Pubmed上取得了最好的结果，GCN-CRF在Citeseer上拥有最佳分类正确率。但是GCN-CRF在Citeseer上分类结果的标准误却大于AHOGE。不难看出，本文提出的三个方法在随机数据集划分情况下，分类正确率和标准误均优于目前的最优方法GCN。Graph-GRU虽然与GCN-CRF在Cora和Pubmed上有相近的分类正确率，Graph-GRU有着更低的标准误，因此Graph-GRU相比于GCN-CRF更稳定。AHOGE在三个数据集上均取得了最低的标准误，说明自适应捕获 高阶依赖使得模型对标记样本位置的影响更鲁棒。

除了训练正确率，另一个倍受关注的是模型的训练效率，即收敛速度与训练时间。下图给出了在随机20次实验情况下，模型在一次迭代的时间、迭代次数和训练总时间上的平均表现。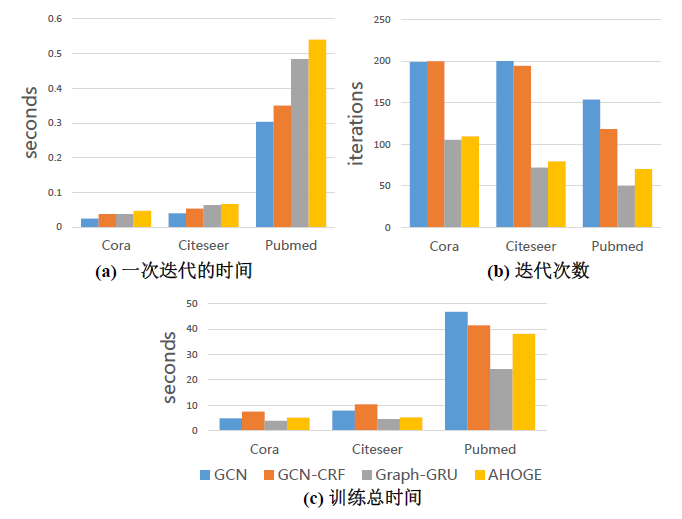

Graph-GRU和AHOGE平均在每一次迭代上所花的时间要多于GCN，但是模型收敛比GCN快，基本迭代次数为GCN的一半，故在模型训练的总时间上所提出的模型都要优于GCN。这里GCN-CRF的短板就体现出来了，因为需要花费更多的迭代次数去求解CRF模块，虽然迭代次数略微少于GCN，但是总时间在Cora和Citeseer上还是要高于GCN的。其次对于Graph-GRU和AHOGE，AHOGE略微比Graph-GRU收敛慢，但是每次迭代花费更多的时间，故总体上的时间开销都要多一些。

敏感性分析

本节对模型中的参数做敏感性分析，主要分为三个方面：（1）标记样本的比例；（2）GCN-CRF模型中CRF迭代次数、Graph-GRU和AHOGE的隐层层数；（3）隐层特征数目。
根据数据集的细节可以看出，上文实验过程中标记样本的比例是很低的，为此，本小节首先讨论了标记样本比例的影响，实验结果如下图所示。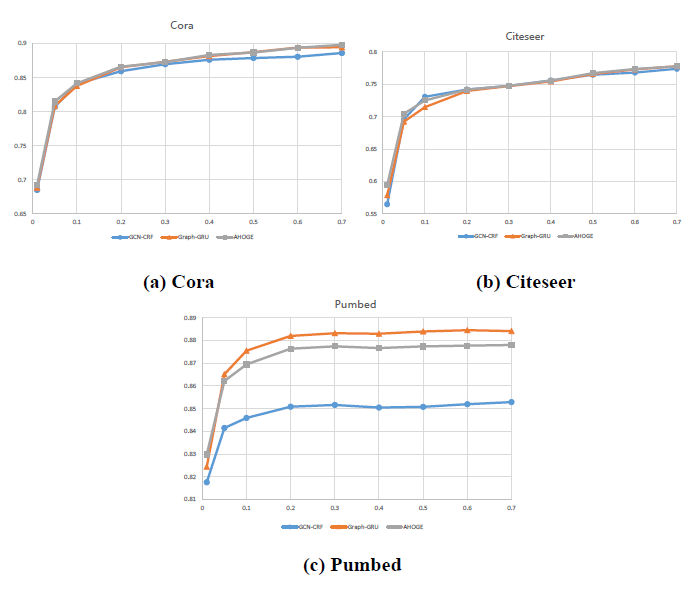

整体上分类正确率随标记样本比例的升高存在一个先升高再平缓的过程。综合标记成本、模型训练开销和分类正确率，数据集只需要20%的标记便可取得很好的结果，这将大大减少标注任务的工作量。同时，GCN-CRF在样本少、图稀疏且标记样本比例小时性能更优，Graph-GRU在数据集大且具备一定比例的标记样本时优于AHOGE，AHOGE在标记样本比例小时更优。

其次，给出CRF的迭代次数和Graph-GRU与AHOGE的隐层数目对模型分类正确率的影响。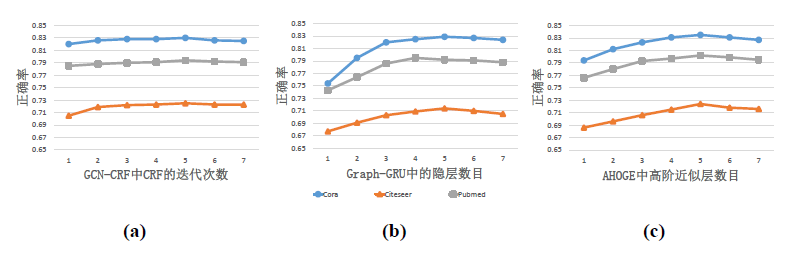

如上文所述，CRF在一般在10次迭代内收敛，上图表明模型在2次迭代后分类正确率就趋于稳定，并在第5次迭代处取得最大值。Graph-GCN和AHOGE模型的结果都有一个先上升再平缓最后再下降的过程，这印证了隐层数目过多会造成编码结果在高阶依赖上过于平滑的现象。Graph-GRU在Cora和Citeseer上最优的隐层数目为5层，在Pubmed上为4层。AHOGE在三个数据集上都在5层高阶近似层上取得最大值。

最后，本文给出隐层特征数目对分类结果的影响。由于Cora数据集与Pubmed数据集的稠密程度相似并有相似的结果趋势，下图以Cora数据集和Citeseer数据集为例展示了隐层特征维度（即编码特征维度）对分类结果的影响。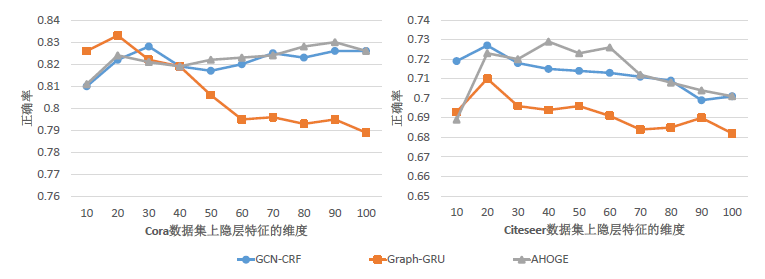

在Cora数据集上，GCN-CRF和AHOGE对隐层特征维度不太敏感，分类正确率相对稳定，而Graph-GRU的分类正确率表现出明显的随隐层特征维度的增加而较少的趋势。 在Citeseer数据集上，三个模型的整体趋势都是先增后降。虽然存在不同维度的特征编码的分类正确率可能一样，但是特征的维度越小，模型的复杂度越低，训练需要的时间相应的越少。

总结

近年来人们越来越关注于关系型数据的学习，图作为一种很自然的关系结构被广泛的用于这类数据的分析与建模。本文关注的是图结构数据上的半监督节点分类这一具备很强现实意义问题。通过对目前相关工作进行分类总结，本文采用目前热门的图编码方法，从编码过程和分类过程两个方面优化目前主流的方法。

具体地，本文首先针对分类过程进行优化并在建模过程中同时利用邻居的特征和标签。本文采用图卷积神经网络GCN来利用邻居特征进行编码，采用条件随机场来平滑GCN的分类结果，并提出GCN-CRF模型。通过将CRF的平均场近似推理构建为RNN模块的形式，GCN-CRF能将该模块挂载在softmax层前面，并在一个统一的模型中端到端地训练编码过程和分类过程。

其次，针对编码过程，为了在特征编码过程中捕获全局信息，本文提出Graph-GRU模型来捕获高阶节点依赖，Graph-GRU通过构建多个前馈RNN层在图上实施GRU来收集邻居的信息。由于节点局部网络结构的差异性，在建模高阶依赖时，容易出现编码的结果过于平滑以致于丢失个体细节特征的现象。基于这个出发点，本文提出了自适应高阶依赖图编码（AHOGE）模型。AHOGE模型首先借用GRU的思想自适应地保留一阶近似，然后堆叠五个高阶接近层来捕获远程节点依赖。 为了自适应地保持高阶近似，AHOGE模型采用高速网络的思想将一阶近似层连接到各个高阶近似层。

最后，在三个基准图结构数据集上的实验表明，本文提出的三个方法在分类正确率和标准误上均优于目前最先进的方法。GCN-CRF更加适合处理图结构相对稀疏的情况，Graph-GRU的收敛较快并且模型的训练时间较少，AHOGE对标记样本在图中的位置更鲁棒并且分类正确率更为稳定。

在实验过程中，本文发现标记节点在图中的位置对模型性能有一定的影响，其造成的分类正确率的差异能高达8%。分析标记节点位置的影响是一个有趣的研究课题，这将作为本文进一步的研究方向。该研究的一个典型应用为基于主动学习的样本标注，通过分析样本所处的位置，挑选出最具信息量和影响力的样本用于标注。通过按这种方式额外挑选一小部分样本，使得模型的性能能得到最大限度的提升，因此能极大的减轻繁重的标注任务。

^{sen2008collective}. SEN P, NAMATA G, BILGIC M, et al., 2008. Collective classification in network data[J]. AI magazine, 29(3): 93. ↩

^{yang2016revisiting}. YANG Z, COHEN W W, SALAKHUTDINOV R, 2016a. Revisiting semi-supervised learning with graph embeddings[J]. arXiv preprint arXiv:1603.08861. ↩

^kipf2016semi. KIPF T N, WELLING M, 2016. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907. ↩

^zhu2003semi. ZHU X, GHAHRAMANI Z, LAFFERTY J D, 2003. Semi-supervised learning using gaussian fields and harmonic functions[C]//Proceedings of the 20th International conference on Machine learning (ICML-03). 912–919. ↩

^lu2003link. LU Q, GETOOR L, 2003. Link-based classification[C]//Proceedings of the 20th International Conference on Machine Learning (ICML-03). 496–503. ↩

^{belkin2006manifold}. BELKIN M, NIYOGI P, SINDHWANI V, 2006. Manifold regularization: A geometric framework for learning from lab ↩

^{perozzi2014deepwalk}. PEROZZI B, AL-RFOU R, SKIENA S, 2014. Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 701–710. ↩

^{grover2016node2vec}. GROVER A, LESKOVEC J, 2016. node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 855–864. ↩

^{weston2012deep}. WESTON J, RATLE F, MOBAHI H, et al., 2012. Deep learning via semi-supervised embedding[M]//Neural Networks: Tricks of the Trade. Springer: 639–655. ↩