MathGraph: A Knowledge Graph for Automatically Solving Mathematical Exercises

一个用于解决高中数学练习题的知识图谱。

MathGraph提出了一种有效的算法，将数学问题与MathGraph对齐，并使用对齐的子图来解决数学练习。

Overview

MathGraph, a knowledge graph aiming to solve high school mathematical exercises.

一个用于解决高中数学练习题的知识图谱。

数学知识图谱与其他领域的知识图谱不一样，需要被特别的设计，原因有如下几点：

1. 数学知识图谱中的知识属于非常特定的领域：需要数学知识，一般基于广泛语义（维基百科等）构建的知识图谱很难获取数学问题中的语义信息。
2. 数学知识图谱中存储的知识应该定义在class-level上，而不是instance-level：一般知识图集中于提取实例，类别以及实例之间的关系。例如，一个三元组（北京，isCaptialOf，中国）显示了两个实例之间的关系。但是，在MathGraph中，原始图中没有实例，只有许多类级别的数学对象（例如，复数，椭圆等）。仅当遇到具体的练习时，才会相应地创建实例。
3. 数学知识图谱应该支持数学推导和计算：数学问题的推理过程不同于其他问题，因为除了逻辑关系外，知识图中还必须包含数学推导来解决数学练习。

对于前两条毋庸置疑，对于第三条，MathGraph是提供了几个推理算法，具体的实操性有待商榷。但是我们在构建数学知识图谱的时候，也应该有这样的念头，我的图谱怎样支持推理？仅仅提供知识点之间的前后依赖关系？大小概念关系？仅仅只提供信息查询我觉得是不够的，支持推理是知识图谱的灵魂。

MathGraph提出了一种有效的算法，将数学问题与MathGraph对齐，并使用对齐的子图来解决数学练习。

这个过程就很符合STC-AOG的理念，构建的MathGraph是完备的AOG，具体的习题过来生成的实例就是一个具体的PG，在PG上做推理，比如代数问题中让所有约束条件得以解决，就解了这个题。

MathGraph

要理解这部分，需要保持面向对象的思想，注意这里的笔记并不完全符合原文，根据我自己的理解做了取舍和修改，感兴趣的可以阅读原文。

定义

数学对象和实例

一个数学概念是一个抽象对象，它有具体的定义、一些属性，可以用作某些运算或派生的目标。

注意，可以根据其他对象来定义数学对象（也就是可以嵌套，比如分数的分子和分母都是有理数）。满足数学对象定义的具体对象称为实例。

不同的数学对象应该有不同的结构，在MathGraph中，数学对象用关键属性（key properties） (p1, p2, · · · , pn)的元组来表示。数学对象的关键属性是可以一起形成和描述该对象实例的所有信息的那些属性。这里列举了几个数学对象：

以复数来说

• 定义：A complex number is a number that can be in the form $a + bi$, where $a$ and $b$ are both real numbers and $i$ is the imaginary unit which satisfies $i^2 = −1$.
• 属性： 复数$a + bi$ 的属性有三个，实部$a$，虚部$b$和$i$。
• 运算：例如，$(a_1 + b_1i) · (a_2 + b_2i) = (a_1a_2 − b_1b_2) + (a_1b_2 + a_2b_1)i$
• 推导：例如，如果$a_1 + b_1 i$和$a_2 + b_2 i$是共轭关系，那么$a_1 = a_2, b_1+b_2=0$

Operation(运算)

通常，运算是一种操作或过程。在给定一个或多个数学对象作为输入（称为操作数）的情况下，该操作或过程产生一个新的对象。简单的例子包括加，减，乘，除和求幂。

Constraint(限制条件)

约束是对一个或多个实例的描述或条件，其中至少一个是不确定的实例。具体有4中限制：

1. 描述限制：比如，复数$x$和$y$共轭
2. 相等限制：$a+2=b$
3. 不等限制：$a^2<5$
4. 集合限制：$a \in N$

对于确定与不确定实例，根据实例是否包含某些不确定值作为其关键属性，可以将实例分为某些实例和不确定实例。如果所有关键属性都是确定的，那么实例就是确定的实例。否则情况不确定。

For example, a real number 2.3 and a function f(x) = x+sin(x) are certain; a complex number 3+ai (where a ∈ R) and a random triangle △ABC are uncertain.

MathGraph结构

MathGraph是一个有向图$G = ⟨V, E⟩ $, 其中$v \in V$是一个数学对象、操作或者限制。边为它们之间的关系。

MathGraph is a directed graph $G = ⟨V, E⟩$, in which each node $v ∈ V $denotes a mathematical object, an operation or a constraint, and each edge $e ∈ E$ is the relation of two nodes.

Nodes

有三种nodes: object nodes, operation nodes and constraint nodes.

Object Nodes An object node $v_o = (t,P,C)$ represents a mathematical object, 其中

• $t$: an instance template of this mathematical object, 实例模板，也就是schema
• $P = (P_1, P_2, \cdots , P_n) $：关键属性（key properties）
• $C$：a set of constraints。根据该定义或某些定理，该数学对象必须满足的一组约束。

Operation Nodes An operation node $v_p = (X_1, X_2, · · · , X_k, Y, f)$ represents a k-ary operation ,其中

• $X_i(i = 1, 2, · · · , k)$ and $Y$ are object nodes representing the domain of the ith operand xi and the result of the operation y respectively,
• $f$：is a function that implements the operation and can be finished by a series of symbolic execution process using a symbolic execution library (e.g. SymPy[10], Mathematica[7]) even if some operands are uncertain instances.

比如获得复数的模就一个Operation，$X_1 = ⟨Complex Number⟩$, $Y = ⟨Real Number⟩$, and $f 4can be implemented by the following symbolic execution process: (1) Get the real part of x1; (2) Get the imaginary part of x1; (3) Return the squared root of the sum of (1) squared and (2) squared.

Constraint Nodes A constraint node $v_c = (d, X_1, X_2, · · · , X_k, f)$ represents a descriptive constraints of k instances, 其中，

• $d$：描述
• $X_i(i = 1, 2, · · · , k)$，涉及的Object
• $f$ : a function which maps this descriptive constraint into several equality constraints, inequality constraints and set constraints.

例如，a constraint node represents that $x_1$ and $x_2$ are a conjugate pair, where $X1 = X2 = ⟨Complex Number⟩$, and f can be implemented by the following process: (1) Get the real part of x1 as a1; (2) Get the real part of x2 as a2; (3) Get the imaginary part of x1 as b1; (4) Get the imaginary part of x2 as b2; (5) Return two equality constraints: a1 = a2 and b1 + b2 = 0.

我觉得Object节点是必须的，但是Operation节点和Constraint节点，在当前我们构建的数学知识图谱中并必须要。

但是，相应的，我们可以有正对性的设计成Object节点这个class的子对象字段。

Edges

有两种边，the derive edges and the flow edges.

The derive edges $E_{derive} = (X,Y,f) $是一种general-special关系，比如从三角形到等腰三角形。 其中f为定义在其两端的限制条件，满足条件才返回true，也就是可以将general节点替换成special节点。

在解决练习时，将实例重新分配给更特定的对象节点将带来对该对象的更多约束，并有助于找到答案。

The flow edge 练习求解过程中实例的流向，这些实例只能从对象节点到操作节点，从操作节点到对象节点或从对象节点到约束节点存在。

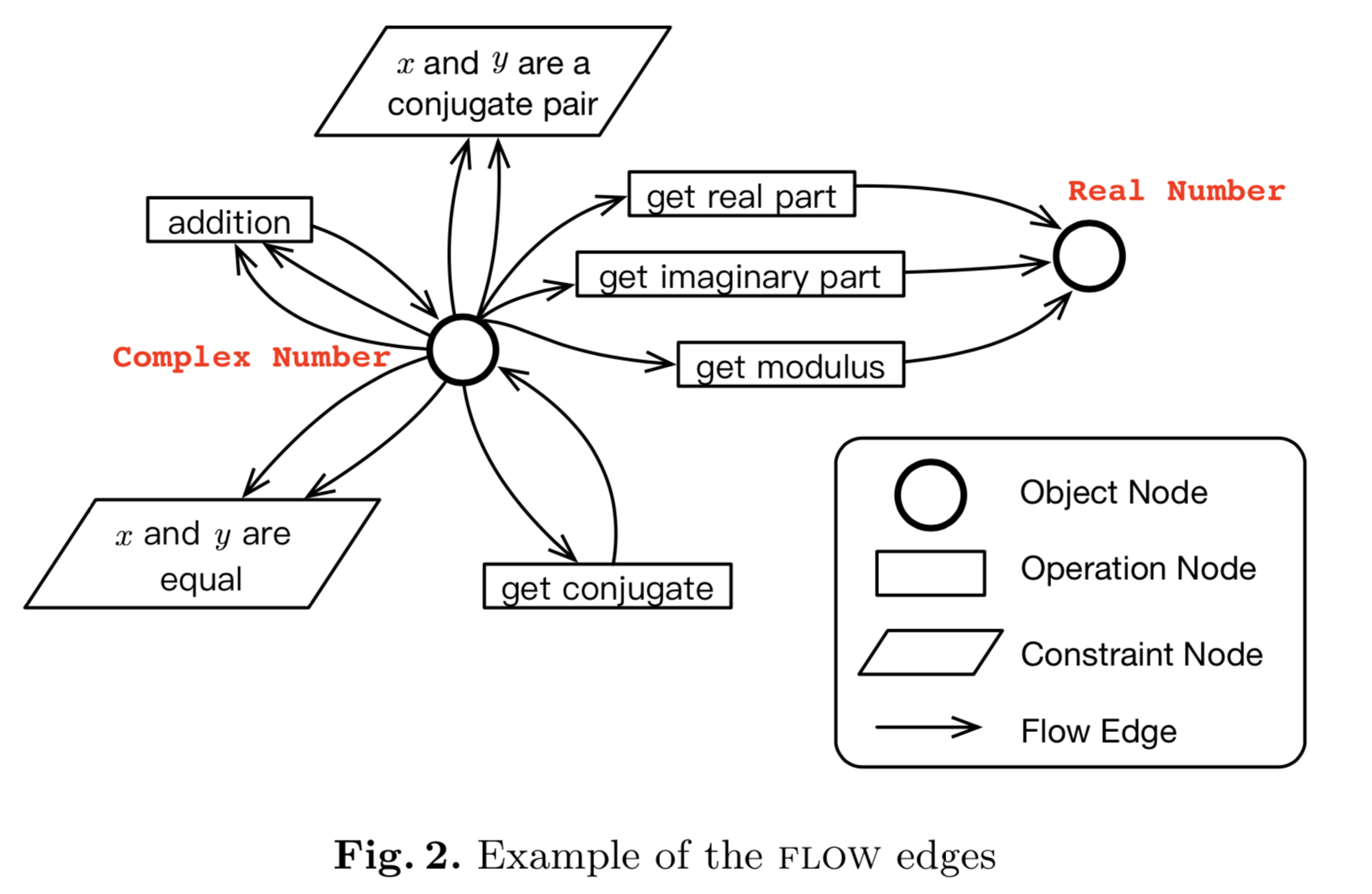
我觉得derive edges是必须的，flow edge反而在目前不需要。derive edges的定义加上节点的定义，让我感觉这很像一个概率图模型，边上定义有function，表示节点之间的转移关系。

解题

解题第一步，将文本的题目parse到MathGraph上。

First, we use a semantic parser mapping exercise text to the instances, operations and constraints respectively. Then, we solve the constraints and update uncertain instances. Finally, we return the answer of this exercise.

parse得到的图其实就是一个pg

这块我们完全可以替换成我们自己的STC-AOG算法，这篇文章提出的解法也并不是很通用，实操性也待商榷，不是我关注的重点，就不做介绍。

实验结果

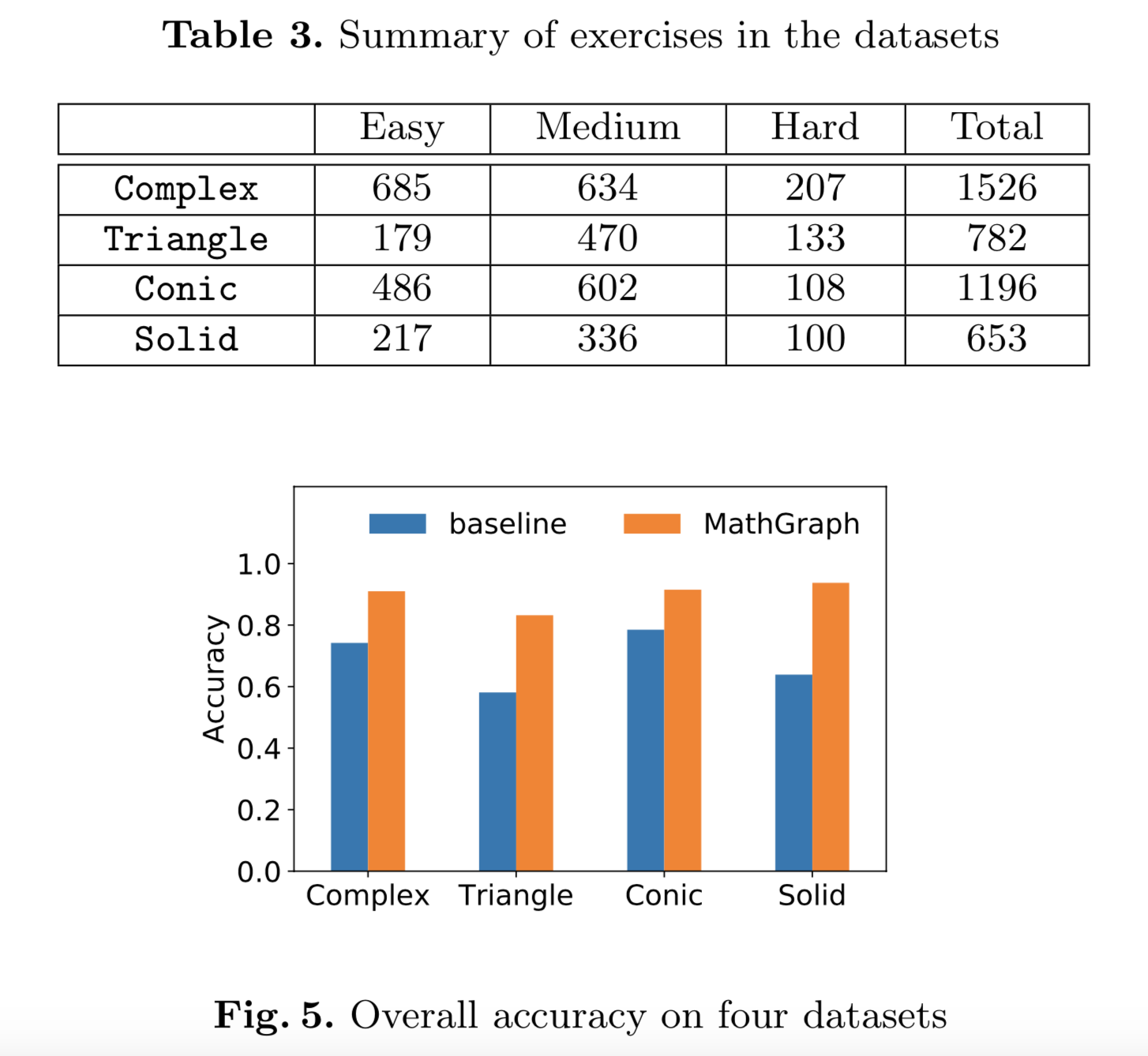
We collect four real-world datasets of mathematical exercises of Chinese high schools, namely Complex, Triangle, Conic and Solid. The exercises are stored in plain text, and the mathematical expressions are stored in the LaTeX format.

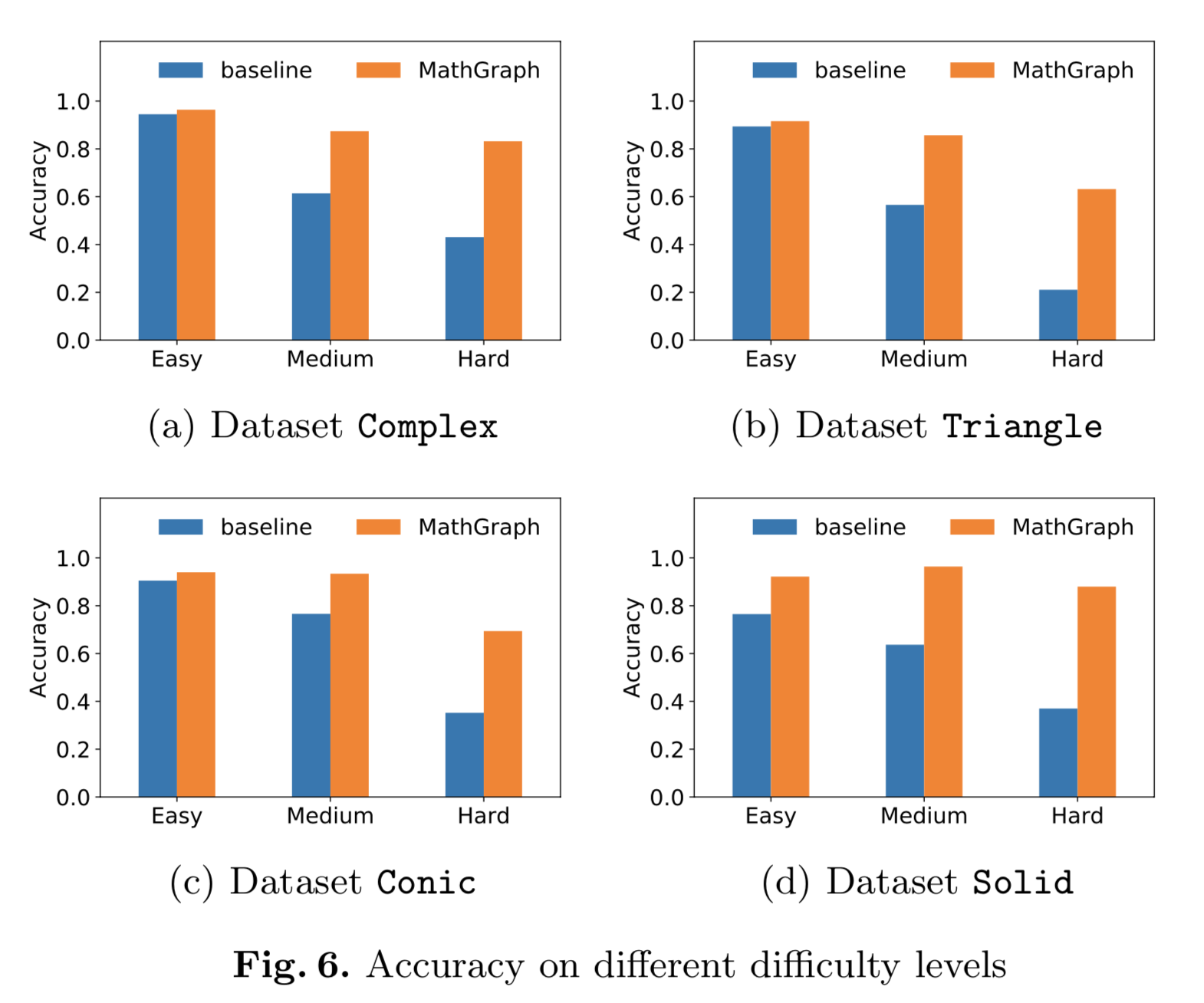
思考

我们的数学知识图谱该怎样建，这篇文章又能给我们什么样的启发。总结下来有如下几点

• 数学知识图谱由于其学科的特殊性、逻辑的严密性、知识点的多样性，采用常规的信息查询方式构建图谱的话，如果不细心处理，估计也就只能查信息了，无法进行推理。
• 推理是知识图谱的灵魂
• 节点的属性可以打开思路，其属性不仅仅只能是干巴巴的文本描述，我们可以放入更多的东西，比如数学性质、定义中的约束，甚至是运算方式。这有点类似复写对象中的比较器、toString等方法。
• 图谱的边也可以打开思路。目前的边只是一个字符串，但是也可以在边上定义属性，甚至是约束条件。比如，一般三角形—->等腰三角形的边上可以有约束条件，比如，两边相等/两角相等。用一个array of string就可以。